题目内容
函数 的零点所在的一个区间是( ).
的零点所在的一个区间是( ).
| A.(-2,-1) | B.(-1,0) | C.(0,1) | D.(1,2) |
C
解析试题分析:因为函数 是R上的连续函数,且f(0)=e0+0-2=-1<0, f(1)=e1+1-2=e-1>0,所以f(0)f(1)<0.所以
是R上的连续函数,且f(0)=e0+0-2=-1<0, f(1)=e1+1-2=e-1>0,所以f(0)f(1)<0.所以 的零点所在的一个区间为(0,1)。
的零点所在的一个区间为(0,1)。
考点:零点存在定理。
点评:本题考查了函数零点的概念与零点定理的应用,零点存在定理只能判断函数在这个区间上是否存在零点,而不能判断零点的个数。属于基础题。

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
曲线 在点P(1,12)处的切线与y轴交点的纵坐标是( )
在点P(1,12)处的切线与y轴交点的纵坐标是( )
| A.-9 | B.-3 | C.9 | D.15 |
函数 ,已知
,已知 在
在 时取得极值,则
时取得极值,则 =
=
| A.2 | B.3 | C.4 | D.5 |
已知函数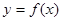 的大致图象如图所示, 则函数
的大致图象如图所示, 则函数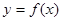 的解析式应为( )
的解析式应为( )
A. | B.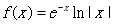 |
C. | D.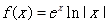 |
曲线 与直线
与直线 所围成图形的面积为( )
所围成图形的面积为( )
| A.2 | B.1 | C. | D. |
已知函数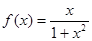 ,则
,则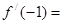
| A.-1 | B.0 | C.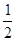 | D.1 |
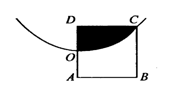
曲线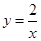 与直线
与直线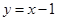 及
及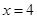 所围成的封闭图形的面积为
所围成的封闭图形的面积为
A.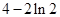 | B.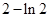 | C.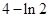 | D.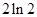 |
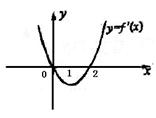
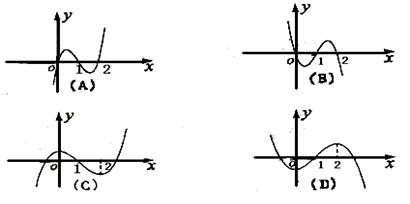
 是函数
是函数 的导函数,
的导函数,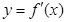 的图象如图所示,则
的图象如图所示,则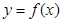 的图象最有可能的是( )
的图象最有可能的是( )