题目内容
由曲线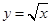 ,直线
,直线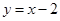 及
及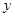 轴所围成的图形的面积为
轴所围成的图形的面积为
A.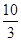 | B.4 | C.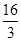 | D.6 |
C
解析试题分析: 根据题意可知,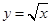 与y=x-2的交点坐标为
与y=x-2的交点坐标为 ,可知交点坐标为(4,2),那么曲边梯形的面积为
,可知交点坐标为(4,2),那么曲边梯形的面积为 ,故选C。
,故选C。
考点:本题主要考查了定积分几何意义的运用,定积分表示曲边梯形的面积的求解运用。
点评:解决该试题的关键是能确定出交点坐标,得到积分的上限和下限,同时能准确表示出被积函数的原函数问题。

练习册系列答案
相关题目
曲线 与直线
与直线 所围成图形的面积为( )
所围成图形的面积为( )
| A.2 | B.1 | C. | D. |
 等于
等于
| A.-2ln2 | B.2ln2 | C.-ln2 | D.ln2 |
已知函数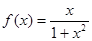 ,则
,则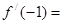
| A.-1 | B.0 | C.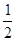 | D.1 |
导函数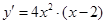 在[-2,2]上的最大值为( )
在[-2,2]上的最大值为( )
A. | B.16 | C.0 | D.5 |
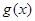 满足:①当
满足:①当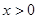 时,
时, 恒成立;②对任意的
恒成立;②对任意的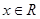 都有
都有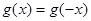 。又函数
。又函数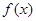 满足:对任意的
满足:对任意的 成立,当
成立,当 时,
时, 。若关于
。若关于 的不等式
的不等式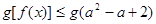 对
对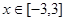 恒成立,则
恒成立,则 的取值范围( )
的取值范围( )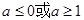
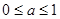
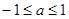
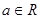
 是定义在R上的函数,其中
是定义在R上的函数,其中 的导函数为
的导函数为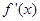 ,满足
,满足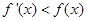 对于
对于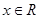 恒成立,则( )
恒成立,则( )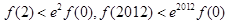
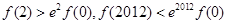
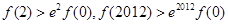
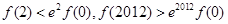



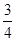
 的对称中心为
的对称中心为 ,记函数
,记函数 的导函数为
的导函数为 ,
, ,则有
,则有 .若函数
.若函数 ,则可求得
,则可求得





