题目内容
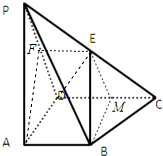
 如图,四棱锥P-ABCD的底面ABCD为一直角梯形,侧面PAD是等边三角形,其中BA⊥AD,CD⊥AD,CD=2AD=2AB=2,平面PAD⊥底面ABCD,E是PC的中点.
如图,四棱锥P-ABCD的底面ABCD为一直角梯形,侧面PAD是等边三角形,其中BA⊥AD,CD⊥AD,CD=2AD=2AB=2,平面PAD⊥底面ABCD,E是PC的中点.(1)求证:BE∥平面PAD;
(2)求证:BE⊥CD;
(3)求三棱锥P-ACD的体积V.
考点:直线与平面平行的判定,棱柱、棱锥、棱台的体积,空间中直线与直线之间的位置关系
专题:综合题,空间位置关系与距离
分析:(1)证BE∥平面PAD,可先构建平面EBM,证明平面EBM∥平面APD,由面面平行,得到线面平行;
(2)取PD的中点F,连接FE,根据线面垂直的判定及性质,及等腰三角形性质,结合线面垂直的判定定理可得AF⊥平面PDC,又由BE∥AF,可得BE⊥平面PDC;
(3)利用VP-ACD=VC-PAD,即可求三棱锥P-ACD的体积V.
(2)取PD的中点F,连接FE,根据线面垂直的判定及性质,及等腰三角形性质,结合线面垂直的判定定理可得AF⊥平面PDC,又由BE∥AF,可得BE⊥平面PDC;
(3)利用VP-ACD=VC-PAD,即可求三棱锥P-ACD的体积V.
解答:
 (1)证明:取CD的中点M,连接EM、BM,则四边形ABMD为矩形
(1)证明:取CD的中点M,连接EM、BM,则四边形ABMD为矩形
∴EM∥PD,BM∥AD;
又∵BM∩EM=M,
∴平面EBM∥平面APD;
而BE?平面EBM,
∴BE∥平面PAD;…(4分)
(2)证明:取PD的中点F,连接FE,则FE∥DC,BE∥AF,
又∵DC⊥AD,DC⊥PA,
∴DC⊥平面PAD,
∴DC⊥AF,DC⊥PD,
∴EF⊥AF,
在Rt△PAD中,∵AD=AP,F为PD的中点,
∴AF⊥PD,又AF⊥EF且PD∩EF=F,
∴AF⊥平面PDC,又BE∥AF,
∴BE⊥平面PDC,
∴CD⊥BE;…(10分)
(3)解:由(2)知∴CD⊥平面PAD,
∵△PAD是边长为1的等边三角形,
∴VP-ACD=VC-PAD=
×
×1×1×sin
×2=
∴三棱锥P-ACD的体积为
…(14分)
 (1)证明:取CD的中点M,连接EM、BM,则四边形ABMD为矩形
(1)证明:取CD的中点M,连接EM、BM,则四边形ABMD为矩形∴EM∥PD,BM∥AD;
又∵BM∩EM=M,
∴平面EBM∥平面APD;
而BE?平面EBM,
∴BE∥平面PAD;…(4分)
(2)证明:取PD的中点F,连接FE,则FE∥DC,BE∥AF,
又∵DC⊥AD,DC⊥PA,
∴DC⊥平面PAD,
∴DC⊥AF,DC⊥PD,
∴EF⊥AF,
在Rt△PAD中,∵AD=AP,F为PD的中点,
∴AF⊥PD,又AF⊥EF且PD∩EF=F,
∴AF⊥平面PDC,又BE∥AF,
∴BE⊥平面PDC,
∴CD⊥BE;…(10分)
(3)解:由(2)知∴CD⊥平面PAD,
∵△PAD是边长为1的等边三角形,
∴VP-ACD=VC-PAD=
| 1 |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| ||
| 6 |
∴三棱锥P-ACD的体积为
| ||
| 6 |
点评:本题考查的知识点是直线与平面平行的判定,直线与平面垂直的判定,考查三棱锥P-ACD的体积,熟练掌握线面平行及线面垂直的判定定理是解答的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
若复数(a2-3a+2)+(a-2)i是纯虚数,则实数a的值为( )
| A、1 | B、2 | C、1或2 | D、-1 |
 如图,在直三棱柱A1B1C1-ABC中,AB⊥BC,E,F分别是A1B,AC1的中点.
如图,在直三棱柱A1B1C1-ABC中,AB⊥BC,E,F分别是A1B,AC1的中点. 如图,四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,SD=AD=2,G是SB的中点.
如图,四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,SD=AD=2,G是SB的中点. 如图在边长为a的正方形ABCD中,E、F分别为边BC、CD中点,设
如图在边长为a的正方形ABCD中,E、F分别为边BC、CD中点,设