题目内容
已知tan(3π-α)=-
,tan(β-α)=-
,则tanβ= .
| 1 |
| 2 |
| 1 |
| 3 |
考点:两角和与差的正切函数
专题:三角函数的求值
分析:直接利用诱导公式化简已知条件,然后利用两角和的正切函数求解即可.
解答:
解:tan(3π-α)=-
,∴tanα=
tan(β-α)=-
,∴
=-
,
可得
=-
,
解得tanβ=
.
故答案为:
;
| 1 |
| 2 |
| 1 |
| 2 |
tan(β-α)=-
| 1 |
| 3 |
| tanβ-tanα |
| 1+tanαtanβ |
| 1 |
| 3 |
可得
tanβ-
| ||
1+
|
| 1 |
| 3 |
解得tanβ=
| 1 |
| 7 |
故答案为:
| 1 |
| 7 |
点评:本题考查两角和的正切函数的应用,诱导公式化简求值,考查计算能力.

练习册系列答案
相关题目
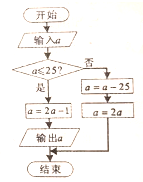 某班有49位同学玩“数字接龙”游戏,具体规则按如图所示的程序框图执行(其中a为座位号),并以输出的值作为下一个输入的值,若第一次 输入的值为8,则第三次输出的值为( )
某班有49位同学玩“数字接龙”游戏,具体规则按如图所示的程序框图执行(其中a为座位号),并以输出的值作为下一个输入的值,若第一次 输入的值为8,则第三次输出的值为( )| A、8 | B、15 | C、29 | D、36 |
已知变量x,y,满足约束条件
,则z=2x-y的最大值为( )
|
| A、2 | B、3 | C、4 | D、6 |
函数f(x)=
的值域为 ( )
| 2x-1 |
| A、[-1,+∞) |
| B、(-∞,-1] |
| C、(-1,-∞) |
| D、[0,+∞) |
已知p:1g(x-1)≥1g(3-x),q:
≥1,则p是q的( )
| 1 |
| x-2 |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知全集A={x∈N|x2+2x-3≤0},B={y|y⊆A},则集合B中元素的个数为( )
| A、2 | B、3 | C、4 | D、5 |