题目内容
求经过三点A(-1,1)、B(1,1)、O(0,0)的圆的方程.
考点:圆的一般方程
专题:直线与圆
分析:经过三点A(-1,1)、B(1,1)、O(0,0)的圆的方程为 x2+y2+dx+ey+f=0,把点的坐标代入求得d、e、f的值,可得所求圆的方程.
解答:
解:设经过三点A(-1,1)、B(1,1)、O(0,0)的圆的方程为 x2+y2+dx+ey+f=0,
则由
求得
,
∴所求的圆的方程为 x2+y2-2y=0.
则由
|
|
∴所求的圆的方程为 x2+y2-2y=0.
点评:本题主要考查利用待定系数法求圆的方程,属于基础题.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
圆x2+y2+2kx+k2-1=0与圆x2+y2+2(k+1)y+k2+2k=0的圆心之间的最短距离是( )
A、
| ||||
B、2
| ||||
| C、1 | ||||
D、
|
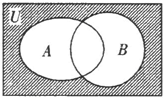 设全集U={1,2,3,4,5,6,7,8},集合A={2,4,5,7},B={1,4,7,8},那么如图所示的阴影部分所表示的集合是( )
设全集U={1,2,3,4,5,6,7,8},集合A={2,4,5,7},B={1,4,7,8},那么如图所示的阴影部分所表示的集合是( )| A、{3,6} |
| B、{4,7} |
| C、{1,2,4,5,7,8} |
| D、{1,2,3,5,6,8} |
根据如图给出的数塔猜测123456×9+7=( )


| A、1111110 |
| B、1111111 |
| C、1111112 |
| D、1111113 |