题目内容
在△ABC中,a、b、c分别为角A、B、C所对的边,且
(2b+c)cosA+acosC =0
(1)求角A的大小:
(2)求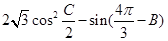 的最大值,并求取得最大值时角 B.C的大小.
的最大值,并求取得最大值时角 B.C的大小.
(1) ;(2)
;(2) 
解析试题分析::(1)此类解三角形的问题,主要使用正余弦定理,将边角互化,对于第一问,通过观察,利用余弦定理,可将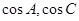 化简,转化成边的关系,然后利用
化简,转化成边的关系,然后利用 ,得到角A的大小;
,得到角A的大小;
(2)通过公式 ,将角
,将角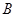 转化成角
转化成角 ,利用两角和的正弦公式展开,化一,得到原式
,利用两角和的正弦公式展开,化一,得到原式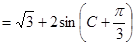 ,根据角
,根据角 的范围,结合三角函数的图像,当
的范围,结合三角函数的图像,当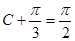 时,取得最大值,得到此时的角
时,取得最大值,得到此时的角 的大小,此题属于基础题型.
的大小,此题属于基础题型.
试题解析:(1)法一: ?
? ,
,
由正弦定理,得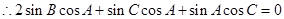 2分
2分
即 ,
, , 4分
, 4分
在 中,
中,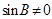 ,
,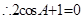 ,即
,即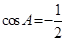 ?又
?又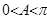 ,所以
,所以 6分
6分
??法二:  ?
?
所以由余弦定理得, 2分??
2分??
化简整理得 ,由余弦定理得
,由余弦定理得 ?? 4分
?? 4分
所以 ,即
,即 ?又
?又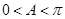 ?所以
?所以 ? 6分
? 6分
(2)∵ ,∴
,∴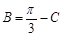 ,
, .
.
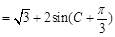 8分
8分
∵ ,∴
,∴ ,∴当
,∴当 ,
, 取最大值
取最大值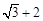 ,此时
,此时 . 12分
. 12分
考点:三角函数的化简与求值

练习册系列答案
相关题目
 中,内角
中,内角 所对的边长分别为
所对的边长分别为 ,
, ,
, ,
, .
. 和
和 的值.
的值.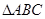 中,已知内角
中,已知内角 ,边
,边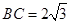 .设内角
.设内角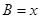 ,面积为
,面积为 .
.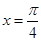 ,求边
,求边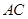 的长;
的长; 中,角A,B,C的对边分别为
中,角A,B,C的对边分别为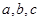 ,且满足
,且满足
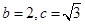 ,求
,求 .
.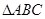 中,内角
中,内角 ,
,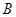 ,
, 所对的边分别为
所对的边分别为 ,
,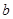 ,
, ,已知
,已知 .
. ,
,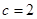 ,求
,求 .
. 中,
中, 分别是角
分别是角 所对的边,且
所对的边,且 .
. ;
; ,求
,求 的取值范围.
的取值范围. ,
,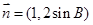 ,
,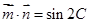 ,其中A,B,C分别为△ABC的三边
,其中A,B,C分别为△ABC的三边 ,
, ,
, 所对的角.
所对的角.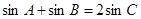 ,且S△ABC=
,且S△ABC= ,求边c的长
,求边c的长 中,内角
中,内角 所对的边分别为
所对的边分别为 .已知
.已知 ,
,
 的大小;
的大小; ,求
,求 中,已知
中,已知 ,
, ,
, ,则
,则 =
=