题目内容
在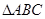 中,已知内角
中,已知内角 ,边
,边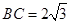 .设内角
.设内角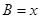 ,面积为
,面积为 .
.
(1)若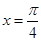 ,求边
,求边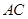 的长;
的长;
(2)求 的最大值.
的最大值.
(1) .(2)
.(2) 取得最大值
取得最大值 .
.
解析试题分析:(1)由正弦定理即可得到 .
.
(2)由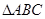 的内角和
的内角和 ,
, 及正弦定理得到
及正弦定理得到 ,将
,将  化简为
化简为
 根据角的范围得到
根据角的范围得到 时,
时, 取得最大值
取得最大值 .
.
试题解析:(1)由正弦定理得: . 6分
. 6分
(2)由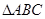 的内角和
的内角和 ,
,
 ,
,
由 8分
8分 =
= 

 10分
10分
因为 ,
,
当 即
即 时,
时, 取得最大值
取得最大值 . 14分
. 14分
考点:正弦定理的应用,和差倍半的三角函数.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
 的内角
的内角 所对的边为
所对的边为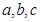 ;则下列命题正确的是
;则下列命题正确的是
 ;则
;则
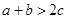 ;则
;则 ;则
;则
 ;则
;则
 ;则
;则
 中,角
中,角 所对的边分别是
所对的边分别是 ,已知
,已知 .
. ,求
,求 ;
; ,
, ,求
,求 .
. ,求△ABC的周长L的取值范围.
,求△ABC的周长L的取值范围. .
. ,求△ABC的周长L的取值范围.
,求△ABC的周长L的取值范围. 中,已知
中,已知 ,向量
,向量 ,
,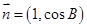 ,且
,且 .
. 的值;
的值; 在边
在边 上,且
上,且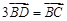 ,
, ,求△
,求△ 的面积.
的面积.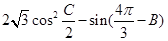 的最大值,并求取得最大值时角 B.C的大小.
的最大值,并求取得最大值时角 B.C的大小. .
.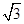 ,c=5,求b.
,c=5,求b. 两地连线上的定点
两地连线上的定点 处建造广告牌
处建造广告牌 ,其中
,其中 为顶端,
为顶端, 长35米,
长35米, 长80米,设
长80米,设 和
和 看
看 .
.
 ,问
,问 求
求