题目内容
在 中,
中, 分别是角
分别是角 所对的边,且
所对的边,且 .
.
(1)求角 ;
;
(2)若 ,求
,求 的周长
的周长 的取值范围.
的取值范围.
(1) ;(2)周长
;(2)周长 的取值范围是
的取值范围是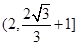 .
.
解析试题分析:(1)条件中的等式 是边角的关系,因此可以考虑采用正弦定理进行边角互化,统一转化为边之间的关系,结合余弦定理的变式,即可求得
是边角的关系,因此可以考虑采用正弦定理进行边角互化,统一转化为边之间的关系,结合余弦定理的变式,即可求得 的大小:
的大小: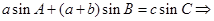
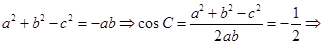
 ;
;
由题意可知,求周长 的取值范围只需求得
的取值范围只需求得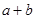 的取值范围即可,而根据(1)中所得的边之间的关系式结合基本不等式即可求得
的取值范围即可,而根据(1)中所得的边之间的关系式结合基本不等式即可求得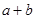 的取值范围:
的取值范围: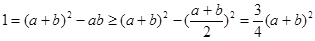
即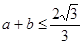 ,又由
,又由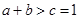 ,从而可知周长
,从而可知周长 的取值范围是
的取值范围是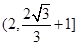 .
.
试题解析:(1)∵ ,∴
,∴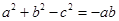 , 3分
, 3分
∴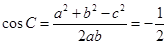 , 6分
, 6分
又∵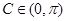 ,∴
,∴ ; 7分
; 7分
(2)由(1)得: , 9分
, 9分
又∵ ,故
,故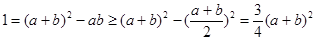 , 11分
, 11分
∴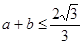 , 12分 又∵
, 12分 又∵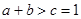 , 13分
, 13分
∴ ,即
,即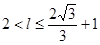 ,∴周长
,∴周长 的取值范围是
的取值范围是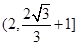 14分
14分
考点: 1.正弦定理余弦定理解三角形;2.基本不等式.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
 .
. ,求△ABC的周长L的取值范围.
,求△ABC的周长L的取值范围.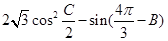 的最大值,并求取得最大值时角 B.C的大小.
的最大值,并求取得最大值时角 B.C的大小. 的三个内角
的三个内角 所对的边分别为
所对的边分别为 ,向量
,向量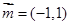 ,
, ,且
,且 .
. 的大小;
的大小;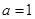 ;②
;② ;③
;③ ,试从中再选择两个条件以确定
,试从中再选择两个条件以确定 .
.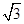 ,c=5,求b.
,c=5,求b. 中,角
中,角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, .
. ,求角
,求角 ,
, ,且△
,且△ ,求
,求 其中
其中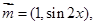
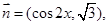 在
在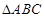 中,
中,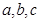 分别是角的对边,且
分别是角的对边,且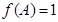 .
.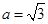 ,
,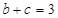 ,求
,求 中,角
中,角 的对边分别为
的对边分别为 ,且
,且 .
.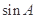 的值;
的值; ,
, ,求向量
,求向量 在
在 方向上的投影.
方向上的投影. 距离为10海里的C处,此时得知,该渔船沿北偏东
距离为10海里的C处,此时得知,该渔船沿北偏东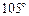 方向,以每小时9海里的速度向一小岛靠近,舰艇时速21海里,则舰艇到达渔船的最短时间是___________.
方向,以每小时9海里的速度向一小岛靠近,舰艇时速21海里,则舰艇到达渔船的最短时间是___________.