题目内容
19.已知F为双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的右焦点,l1,l2为C的两条渐近线,点A在l1上,且FA⊥l1,点B在l2上,且FB∥l1,若$|{FA}|=\frac{4}{5}|{FB}|$,则双曲线C的离心率为( )| A. | $\sqrt{5}$ | B. | $\frac{{\sqrt{5}}}{2}$ | C. | $\frac{{\sqrt{5}}}{2}$或$\frac{{3\sqrt{5}}}{2}$ | D. | $\frac{{\sqrt{5}}}{2}$或$\sqrt{5}$ |
分析 设右焦点F(c,0),双曲线的两条渐近线方程为l1:y=$\frac{b}{a}$x,l2:y=-$\frac{b}{a}$x.由点到直线的距离公式,计算可得|FA|,再由两直线平行的条件:斜率相等,可得直线FB的方程,联立直线l2,可得交点B的坐标,运用两点的距离公式,化简整理,结合离心率公式,计算即可得到所求值.
解答 解:设F(c,0),双曲线的两条渐近线方程为l1:y=$\frac{b}{a}$x,l2:y=-$\frac{b}{a}$x.①
则F到直线l1的距离|FA|=$\frac{|bc-0|}{\sqrt{{a}^{2}+{b}^{2}}}$=$\frac{bc}{c}$=b,
由FB∥l1,可得直线FB的方程为y=$\frac{b}{a}$(x-c),②
由①②可得x=$\frac{1}{2}$c,y=-$\frac{bc}{2a}$,
即有B($\frac{1}{2}$c,-$\frac{bc}{2a}$),
|FB|=$\sqrt{(c-\frac{1}{2}c)^{2}+(\frac{bc}{2a})^{2}}$=$\frac{1}{2}$c$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}$=$\frac{1}{2}$•$\frac{{c}^{2}}{a}$,
由$|{FA}|=\frac{4}{5}|{FB}|$,
可得b=$\frac{4}{5}$•$\frac{1}{2}$•$\frac{{c}^{2}}{a}$,即2c2=5ab,
两边平方可得4c4=25a2b2=25a2(c2-a2),
由e=$\frac{c}{a}$,可得4e4-25e2+25=0,
解得e2=5或e2=$\frac{5}{4}$,
即为e=$\sqrt{5}$或e=$\frac{\sqrt{5}}{2}$.
故选:D.
点评 本题考查双曲线的离心率的求法,注意运用渐近线方程和点到直线的距离公式,以及两直线平行的条件:斜率相等,考查化简整理的运算能力,属于中档题.

 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | i | B. | -i | C. | -1 | D. | 1 |
 一台机器使用的时间较长,但还可以使用,它按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产的零件中有缺点的零件数随机器运转的速度而变化,如表为抽样数据:
一台机器使用的时间较长,但还可以使用,它按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产的零件中有缺点的零件数随机器运转的速度而变化,如表为抽样数据:| 转速x(转/秒) | 16 | 14 | 12 | 8 |
| 每小时生产有缺点的零件数y(件) | 11 | 9 | 8 | 5 |
(Ⅱ)根据散点图判断,y=ax+b与$y=c\sqrt{x}+d$哪一个适宜作为每小时生产的零件中有缺点的零件数y关于转速x的回归方程类型 (给出判断即可,不必说明理由),根据判断结果及表中数据,建立y关于x的回归方程;
(Ⅲ)若实际生产中,允许每小时生产的零件中有缺点的零件数最多为10个,那么机器的运转速度应控制在什么范围内?
(参考公式:$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}$,$\hat a=\overline y-\hat b\overline x$.)
| A. | $\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | $\sqrt{13}$ | D. | $\sqrt{15}$ |
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{2}}}{4}$ |
| A. | $\sqrt{29}$-$\sqrt{13}$ | B. | 5+$\sqrt{13}$ | C. | 2$\sqrt{7}$+$\sqrt{13}$ | D. | $\sqrt{29}$+$\sqrt{13}$ |
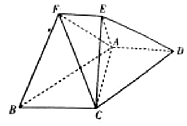 已知多面体ABCDEF中,四边形ABCD为平行四边形,AD⊥平面AEC,且$AC=\sqrt{2}$,AE=EC=1,AD=2EF,EF∥AD.
已知多面体ABCDEF中,四边形ABCD为平行四边形,AD⊥平面AEC,且$AC=\sqrt{2}$,AE=EC=1,AD=2EF,EF∥AD.