题目内容
正方形ABCD、ABEF的边长都是1，而且平面ABCD与平面ABEF互相垂直，点M在AC上移动，点N在BF上移动，若CM=BN=a(0＜a＜
),(1)求MN的长；(2)求a为何值时，MN的长最小.
解析：∵面ABCD⊥面ABEF，
面ABCD∩面ABEF=AB，AB⊥BE，
∴BE⊥面ABC.
∴AB、BC、BE两两垂直.
∴以B为原点，以BA、BE、BC所在直线为x轴，y轴和z轴，建立如图所示空间直角坐标系.
∴则
,
.
∴
.
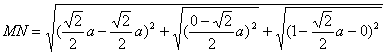
∴当a=
时，|MN|最短，为
，此时，M、N恰为AC、BF的中点.
练习册系列答案
相关题目
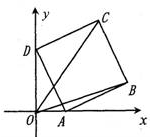如图放置的正方形ABCD，AB=1，A，D分别在x，y轴的正半轴上（含坐标原点）滑动，则
如图，BD是正方形ABCD的对角线，
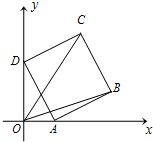（2013•临沂三模）如图放置的正方形ABCD，AB=1，A，D分别在x轴、y轴的正半轴（含原点）上滑动，则