题目内容
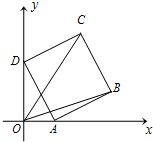 (2013•临沂三模)如图放置的正方形ABCD,AB=1,A,D分别在x轴、y轴的正半轴(含原点)上滑动,则
(2013•临沂三模)如图放置的正方形ABCD,AB=1,A,D分别在x轴、y轴的正半轴(含原点)上滑动,则| OC |
| OB |
2
2
.分析:设∠DAO=θ,则∠BAx=
-θ,OA=cosθ,OD=sinθ,求得点B(cosθ+sinθ,cosθ),点C(sinθ,cosθ+sinθ),计算
•
等于1+sin2θ≤2,可得
•
的最大值.
| π |
| 2 |
| OB |
| OC |
| OB |
| OC |
解答:解:设∠DAO=θ,则∠BAx=
-θ,∴OA=cosθ,OD=sinθ,
∴点B(cosθ+sinθ,cosθ),过点C作y轴的垂线CE,E为垂足,则∠CDE=θ,
由此可得点C(sinθ,cosθ+sinθ).
∴
•
=(cosθ+sinθ)sinθ+cosθ(cosθ+sinθ)=sin2θ+cos2θ+2sinθcosθ=1+sin2θ≤2,
故
•
的最大值为2,
故答案为 2.
| π |
| 2 |
∴点B(cosθ+sinθ,cosθ),过点C作y轴的垂线CE,E为垂足,则∠CDE=θ,
由此可得点C(sinθ,cosθ+sinθ).
∴
| OB |
| OC |
故
| OB |
| OC |
故答案为 2.
点评:本题主要考查两个向量的数量积的运算,求得点C(sinθ,cosθ+sinθ),是解题的难点和关键,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2013•临沂三模)甲、乙两名运动员在某项测试中的6次成绩如茎叶图所示,
(2013•临沂三模)甲、乙两名运动员在某项测试中的6次成绩如茎叶图所示, (2013•临沂三模)如图是函数f(x)=x2+ax+b的部分图象,函数g(x)=ex-f'(x)的零点所在的区间是(k,k+1)(k∈z),则k的值为( )
(2013•临沂三模)如图是函数f(x)=x2+ax+b的部分图象,函数g(x)=ex-f'(x)的零点所在的区间是(k,k+1)(k∈z),则k的值为( ) (2013•临沂三模)函数y=sin(πx+φ)(φ>0)的部分图象如图所示,设P是图象的最高点,A,B是图象与x轴的交点,则tan∠APB=( )
(2013•临沂三模)函数y=sin(πx+φ)(φ>0)的部分图象如图所示,设P是图象的最高点,A,B是图象与x轴的交点,则tan∠APB=( )