题目内容
已知集合A={x|x2-(2+4m)x+8m=0},B={x|x<0},若命题“A∩B=∅”是假命题,求实数m的取值范围.
考点:交集及其运算
专题:集合
分析:由命题“A∩B=∅”是假命题,得到A∩B≠∅,即方程x2-(2+4m)x+8m=0至少有一个负根,然后分方程的两个根均为负值,和一正一负分类求解实数m的取值范围.
解答:
解:∵A∩B=∅是假命题,
∴A∩B≠∅.
∵B={x|x<0},
方程x2-(2+4m)x+8m=0的判别式△=(2+4m)2-32m=4(2m-1)2≥0,
若方程x2-(2+4m)x+8m=0的两根x1,x2均非负,则有
,解得m∈∅;
若方程x2-(2+4m)x+8m=0的两根x1,x2一正一负,
则f(0)=8m<0,即m<0.
综上,实数m的取值范围是{m|m<0}.
∴A∩B≠∅.
∵B={x|x<0},
方程x2-(2+4m)x+8m=0的判别式△=(2+4m)2-32m=4(2m-1)2≥0,
若方程x2-(2+4m)x+8m=0的两根x1,x2均非负,则有
|
若方程x2-(2+4m)x+8m=0的两根x1,x2一正一负,
则f(0)=8m<0,即m<0.
综上,实数m的取值范围是{m|m<0}.
点评:本题考查了交集及其运算,考查了数学转化思想方法及分类讨论的数学思想方法,考查了一元二次方程的根与系数的关系,是基础题.

练习册系列答案
相关题目
函数y=
的值域是( )
| 16-4x |
| A、[0,+∞) |
| B、[0,4] |
| C、[0,4) |
| D、(0,4) |
如果执行图中的程序框图,那么输出的n为( )


| A、5 | B、6 | C、7 | D、8 |
已知集合A={x|x2-2x<0},B={x|-
<x<
},则( )
| 5 |
| 5 |
| A、A∩B=∅ | B、A∪B=R |
| C、B⊆A | D、A⊆B |
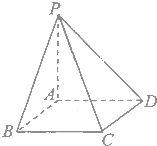 如图,四棱锥P-ABCD的底面ABCD是边长为l的正方形,侧棱PA=1,PB=PD=
如图,四棱锥P-ABCD的底面ABCD是边长为l的正方形,侧棱PA=1,PB=PD=| 2 |
| A、3对 | B、4对 | C、5对 | D、6对 |
 如图,某几何体的下部分是长为8,宽为6,高为3的长方体,上部分是侧棱长都相等且高为3的四棱锥,求:
如图,某几何体的下部分是长为8,宽为6,高为3的长方体,上部分是侧棱长都相等且高为3的四棱锥,求: