题目内容
某商家举办购物抽奖活动,盒中有大小相同的9张卡片,其中三张标有数字1,两张标有数字0,四张标有数字-1,先从中任取三张卡片,将卡片上的数字相加,设数字和为n,当n>0时,奖励奖金10n元;当n≤0,无奖励.
(1)求取出的三个数字中恰有一个-1的概率.
(2)设x为奖金金额,求x的分布列和期望.
(1)求取出的三个数字中恰有一个-1的概率.
(2)设x为奖金金额,求x的分布列和期望.
考点:离散型随机变量及其分布列,离散型随机变量的期望与方差
专题:概率与统计
分析:(1)利用排列组合公式,我们易计算出“该幸运观众摸球三次就停止”的个数,及所有事件的总个数,代入古典概型公式,即可得到答案.
(2)根据题意可得X的可能值为0,10,20,30,分别计算出X分别取0,10,20,30时的概率,可得到X的分布列,代入期望公式求出数学期望EX的值.
(2)根据题意可得X的可能值为0,10,20,30,分别计算出X分别取0,10,20,30时的概率,可得到X的分布列,代入期望公式求出数学期望EX的值.
解答:
解:(1)设“取出的三个数字中恰有一个-1”为事件A,由题意知是一个等可能事件的概率,
试验发生的所有事件是从9张卡片中取三个,共有C93种结果,而事件A是取到只有一个-1,共有C41C52,
则P(A)=
=
,
(2)X的可能取值是:0,10,20,30,其概率计算与(1)解释同理.
①任取三张卡片都是-1,或任取三张卡片中两张是-1、一张是0,或任取三张卡片中两张是-1、一张是1,
任取三张卡片中两张是0、一张是-1,或任取三张卡片中以张是-1、一张是0、一张是1,
则P(X=0)=
=
,
②任取三张卡片中两张是1、一张是-1,或任取三张卡片中两张是0、一张是1,
则P(X=10)=
=
,
③任取三张卡片中两张是1、一张是0,则P(X=20)=
=
,
④任取三张卡片都是1,则P(X=30)=
=
,
∴X的分布列为:
∴EX=0+10×
+20×
+30×
=
.
试验发生的所有事件是从9张卡片中取三个,共有C93种结果,而事件A是取到只有一个-1,共有C41C52,
则P(A)=
| ||||
|
| 10 |
| 21 |
(2)X的可能取值是:0,10,20,30,其概率计算与(1)解释同理.
①任取三张卡片都是-1,或任取三张卡片中两张是-1、一张是0,或任取三张卡片中两张是-1、一张是1,
任取三张卡片中两张是0、一张是-1,或任取三张卡片中以张是-1、一张是0、一张是1,
则P(X=0)=
| ||||||||||||||||||||
|
| 31 |
| 42 |
②任取三张卡片中两张是1、一张是-1,或任取三张卡片中两张是0、一张是1,
则P(X=10)=
| ||||||||
|
| 5 |
| 28 |
③任取三张卡片中两张是1、一张是0,则P(X=20)=
| ||||
|
| 1 |
| 14 |
④任取三张卡片都是1,则P(X=30)=
| ||
|
| 1 |
| 84 |
∴X的分布列为:
| X | 0 | 10 | 20 | 30 | ||||||||
| P |
|
|
|
|
| 5 |
| 28 |
| 1 |
| 14 |
| 1 |
| 84 |
| 25 |
| 7 |
点评:本题考查等可能事件的概率,离散型随机变量及其分布列、期望,要注意不重不漏,这是解答本题的易错点,熟练掌握古典概型的意义及概率计算公式、分类讨论的思想方法、随机变量的分布列和数学期望是解题的关键.

练习册系列答案
相关题目
设全集U={x∈Z|-2≤x≤2},集合A={x|x2=1},B={x∈Z|x2-2x≤0},则A∩(∁UB)=( )
| A、∅ | B、{1} |
| C、{-1} | D、{-1,1} |
下列说法中正确的有( )
①若任取x1,x2∈I,当x1<x2时,f (x1)<f (x2),则y=f (x)在I上是增函数;
②函数y=x2在R上是增函数;
③函数y=-
在定义域上是增函数;
④y=
的单调递减区间是(-∞,0)∪(0,+∞).
①若任取x1,x2∈I,当x1<x2时,f (x1)<f (x2),则y=f (x)在I上是增函数;
②函数y=x2在R上是增函数;
③函数y=-
| 1 |
| x |
④y=
| 1 |
| x |
| A、0个 | B、1个 | C、2个 | D、3个 |
若a>1,b>-1,则下列不等式成立的是( )
| A、a>b | B、ab>-1 |
| C、a>-b | D、a-b>2 |
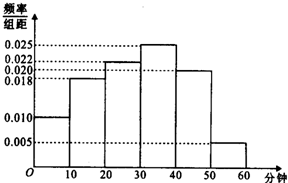 电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名.右图是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图.将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”,已知“体育迷”中有10名女性.
电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名.右图是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图.将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”,已知“体育迷”中有10名女性.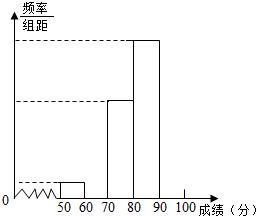 中日“钓鱼岛争端”问题越来越引起社会关注,我校对高一600名学生进行了一次“钓鱼岛”知识测试,并从中抽取了部分学生的成绩(满分100分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.
中日“钓鱼岛争端”问题越来越引起社会关注,我校对高一600名学生进行了一次“钓鱼岛”知识测试,并从中抽取了部分学生的成绩(满分100分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.