题目内容

中心在原点，对称轴为坐标轴，离心率为
1
2
，长轴长为8的椭圆方程为（　　）
A、
y2
16
+
x2
12
=1
B、
x2
16
+
y2
12
=1
C、
y2
16
+
x2
12
=1或
x2
16
+
y2
12
=1
D、不存在
考点：椭圆的标准方程
专题：圆锥曲线的定义、性质与方程
分析：利用椭圆的简单性质求解．
解答： 解：当对称轴为x轴时，设椭圆方程为
x2
a2
+
y2
b2
=1，a＞b＞0，
由已知得
c
a
=
1
2
2a=8
a2=b2+c2
，
解得a=4，b=2
3
，
∴椭圆方程为
x2
16
+
y2
12
=1．
当对称轴为y轴时，设椭圆方程为
x2
b2
+
y2
a2
=1，a＞b＞0，
由已知得
c
a
=
1
2
2a=8
a2=b2+c2
，
解得a=4，b=2
3
，
∴椭圆方程为
x2
12
+
y2
16
=1．
故选：C．
点评：本题考查椭圆方程的求法，是基础题，解题时要注意椭圆的简单性质的合理运用．
练习册系列答案
相关题目
已知函数f（x）是函数y=-
x
的反函数，则函数f（x）图象上点x=-1处切线的方程为
 
．
函数y=log2x与函数y=log2（x-2）的图象及y=-2与y=-3所围成的图形面积是_
 
．
设函数f（x）=
a
•
b
，其中向量
a
=（m，cos2x），
b
=（1+sinxcosx，1），x∈R，且函数y=f（x）的图象过点（
π
4
，-1）．
（1）求实数m的值；
（2）求函数f（x）的最大值及此时x值的集合；
（3）求函数f（x）的图象中，求出离坐标轴y轴最近的对称方程．
若直线y=mx是y=lnx+1的切线，则m=（　　）
A、1B、2C、0D、4
如图是某同学用于计算S=sin1+sin2+sin3+…+sin2012值的程序框图，则在判断框中填写（　　）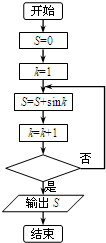
A、k＞2011？
B、k＞2012？
C、k＜2011？
D、k＜2012？
已知c＜0，在下列不等式中成立的是（　　）
A、2c＞1
B、c＞（
1
2
）c
C、2c＜（
1
2
）c
D、2c＞（
1
2
）c
在等差数列{an}中，若a1，a4是方程x2-x-6=0的两根，则a2+a3的值为（　　）
A、6B、-6C、-1D、1
椭圆的中心在原点，对称轴为坐标轴，焦点在x轴上，以椭圆的短轴的一个端点B与两个焦点F1、F2为顶点的三角形的周长是8+4
3
，且∠BF1F2=
π
6
．
（1）求椭圆的标准方程；
（2）若直线y=x+1与椭圆交于点M、N，求线段|MN|的长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网