题目内容
对于实数x,y,若|x-1|≤2,|y-2|≤1,则|x-2y+1|的最大值为( )
| A、4 | B、6 | C、8 | D、10 |
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,利用目标函数的几何意义,进行求最值即可.
解答:
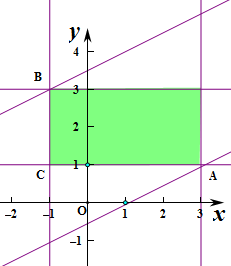 解:∵|x-1|≤2,|y-2|≤1,
解:∵|x-1|≤2,|y-2|≤1,
∴-1≤x≤3,1≤y≤3,
作出不等式组对应的平面区域如图(阴影部分):
设z=x-2y+1,则y=
x-
+
,平移直线y=
x-
+
,
由图象可知当直线y=
x-
+
,过点B(-1,3)时,直线y=
x-
+
的截距最大,此时z最小,代入目标函数z=x-2y+1,得z=-6,
当直线y=
x-
+
,过点A(3,3)时,直线y=
x-
+
的截距最小,此时z最大,代入目标函数z=x-2y+1,得z=-2,
即-6≤z≤-2,
则2≤|z|≤6,则|x-2y+1|的最大值为6.
故选:B
 解:∵|x-1|≤2,|y-2|≤1,
解:∵|x-1|≤2,|y-2|≤1,∴-1≤x≤3,1≤y≤3,
作出不等式组对应的平面区域如图(阴影部分):
设z=x-2y+1,则y=
| 1 |
| 2 |
| z |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| z |
| 2 |
| 1 |
| 2 |
由图象可知当直线y=
| 1 |
| 2 |
| z |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| z |
| 2 |
| 1 |
| 2 |
当直线y=
| 1 |
| 2 |
| z |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| z |
| 2 |
| 1 |
| 2 |
即-6≤z≤-2,
则2≤|z|≤6,则|x-2y+1|的最大值为6.
故选:B
点评:本题主要考查线性规划的基本应用,利用目标函数的几何意义是解决问题的关键,利用数形结合是解决问题的基本方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在一次抗洪抢险中,用射击方法引爆从上游漂流而下一巨大汽油罐.已知只有5发子弹备用,且首次命中只能使汽油流出,再次命中才能引爆成功.每次射击命中概率都是
,每次命中与否互相独立,则油罐被引爆的概率为( )
| 2 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
若a<b,则下列不等式中正确的是( )
| A、ac<bc | ||||
B、
| ||||
| C、a-c<b-c | ||||
| D、a+c>b+c |
已知函数y=2sin(ωx+φ)(φ>0)为偶函数(0<φ<π),其图象与直线y=2某两个交点的横坐标分别为x1,x2,若|x1-x2|的最小值为π,则该函数的一个递增区间可以是( )
A、(-
| ||||
B、(-
| ||||
C、(0,
| ||||
D、(
|
角α的终边过P(sin
,cos
),则角α的最小正值是( )
| 2π |
| 3 |
| 2π |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
在△ABC中,若|
|=3,|
|=4,∠BAC=60°,则
•
=( )
| AB |
| AC |
| BA |
| AC |
| A、6 | B、4 | C、-6 | D、-4 |
已知集合A={5,10,15,20},B={5,15,25},则A∩B=( )
| A、{5,15} |
| B、{5,10,15,20,25} |
| C、{10,20} |
| D、{25} |
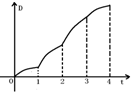
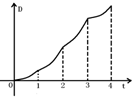
 如图放置的边长为1的正方形PABC沿x轴正方向滚动.设顶点P(x,y)的轨迹方程是y=f(x),设y=f(x)在其两个相邻零点间的图象与x轴所围区域为S,则直线x=t从t=0到t=4所匀速移动扫过区域S的面积D与t的函数图象大致为( )
如图放置的边长为1的正方形PABC沿x轴正方向滚动.设顶点P(x,y)的轨迹方程是y=f(x),设y=f(x)在其两个相邻零点间的图象与x轴所围区域为S,则直线x=t从t=0到t=4所匀速移动扫过区域S的面积D与t的函数图象大致为( )