题目内容

化简根式
4-x13
的结果为（　　）
A、x3•
4x
B、x3•
4-x
C、-x3•
4x
D、-x3•
4-x
考点：根式与分数指数幂的互化及其化简运算
专题：函数的性质及应用
分析：由于根式
4-x13
有意义，可得-x13≤0，变形
4(-x3)4•(-x)
，即可得出．
解答： 解：根式
4-x13
=
4(-x3)4•(-x)
=-x3•
4-x
．
故选：D．
点评：本题考查了根式的定义域及其运算性质，属于基础题．
练习册系列答案
相关题目
已知a，b为正常数，且a+b=2．设0＜x＜1，则y=
a2
x
+
b2
1-x
的最小值为
 
．
化简：
（1）lg22+lg5lg2+lg5；
（2）[(1-log63)2+log62•log618]÷log64；
（3）5log25(lg22+lg
5
2
)；
（4）log23•log35•log58；
（5）（log32+
1
log43
）（log26-1）
向量
a
=（1，x），
b
=（-2，1），若
a
⊥
b
，则|
a
|=（　　）
A、
5
B、5
C、3
D、2
在平面直角坐标系中，若点M，N同时满足：①点M，N都在函数y=f（x）图象上；②点M，N关于原点对称，则称点对（M，N）是函数y=f（x）的一个“望点对”（规定点对（M，N）与点对（N，M）是同一个“望点对”）．那么函数f（x）=
1
x
  (x＞0)
-x2-2x
 (x≤0)
的“望点对”的个数为
 
．
函数f（x）=
2
+
1
x2-2x+3
的值域是
 
．
已知点（1，-1）和（-2，1）在直线3x-2y-a=0的两侧，则a的取值范围是（　　）
A、（-5，8）
B、（-8，5）
C、（-∞，-5）∪（8，+∞）
D、（-∞，-8）∪（5，+∞）
复数z=
3+i
1-i
（i为虚数单位）的虚部为
 
．
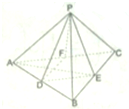如图，在所有棱长都相等的正三棱锥P-ABC中，D，E，F分别是AB，BC，CA的中点，下列四个结论不成立的是（　　）
A、BC∥平面PDF
B、平面PDF⊥平面ABC
C、平面PAE⊥平面ABC
D、平面PDF⊥平面PAE

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网