题目内容
从一块半径为R的半圆形钢板上截取一块矩形钢板，求矩形钢板面积的最大值．
考点：基本不等式
专题：不等式的解法及应用
分析：如图所示，设∠AOB=θ，则AB=Rsinθ，BC=2Rcosθ．可得S矩形ABCD=AB•BC=Rsinθ•2Rcosθ=R2sin2θ，再利用正弦函数的单调性即可得出．
解答：
解：如图所示，
设∠AOB=θ，则AB=Rsinθ，BC=2Rcosθ．
∴S矩形ABCD=AB•BC=Rsinθ•2Rcosθ=R2sin2θ≤R2，
当且仅当θ=
时取等号．
∴矩形钢板面积的最大值是R2．
设∠AOB=θ，则AB=Rsinθ，BC=2Rcosθ．
∴S矩形ABCD=AB•BC=Rsinθ•2Rcosθ=R2sin2θ≤R2，
当且仅当θ=
| π |
| 4 |
∴矩形钢板面积的最大值是R2．
点评：本题考查了利用三角函数的单调性求矩形面积的最大值，属于基础题．
练习册系列答案
相关题目
复数z=
为纯虚数，则实数a的值为（ ）
| a+i |
| 4+3i |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
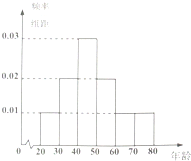“行通济”是广东佛山一带在元宵节期间举行的游玩祈福活动，每到这一天，家家户户都会扶老携幼，自清晨到夜幕，举着风车、摇着风铃、拎着生菜浩浩荡荡地由北到南走过通济桥，祈求来年平平安安、顺顺利利．为了了解不同年龄层次的人对这一传统习俗的参与度，现随机抽取年龄在20～80岁之间的60人，并按年龄层次[20，30），[30，40），[40，50），[50，60），[60，70），[70，80）绘制频率分布直方图如图所示，其中参与了2014年“行通济”活动的人数如下表．若规定年龄分布在[20，60）岁的为“中青年人”，60岁以上（含60岁）为“老年人”．