题目内容
19.若函数f(x)在[m,n](m<n)上的值域恰好为[m,n],则称f(x)为函数的一个“等值映射区间”.下列函数:①y=x2-1;②y=2+log2x;③y=2x-1;④$y=\frac{1}{x-1}$.其中,存在唯一一个“等值映射区间”的函数有2个.分析 若函数f(x)在[m,n](m<n)上的值域恰好为[m,n],则称f(x)为函数的一个“等值映射区间”.根据新定义可知,“等值映射区间”即是函数与另一函数y=x有两个交点.即可判断.
解答 解:根据新定义可知,“等值映射区间”即是函数与另一函数y=x有两个交点.[m,n](m<n)上的值域恰好为[m,n],可见[m,n]是单调递增.
对于①y=x2-1;根据新定义可得:x2-1=x,方程有两个解,即函数y=x2-1与函数y=x有两个交点.但在同一增区间上只有一个,故①不是;
对于②y=2+log2x;根据新定义可得:2+log2x=x,即函数y=2+log2x与函数y=x有两个交点.且在定义域内都是递增,故②是;
对于③y=2x-1;根据新定义可得:2x-1=x,即函数y=2x-1与函数y=x有两个交点.且在定义域内都是递增,故③是;
对于④$y=\frac{1}{x-1}$;根据新定义可得:x2-x=1,方程有两个解,即函数$y=\frac{1}{x-1}$与函数y=x有两个交点.但在同一增区间是只有一个,故④不是;
故答案为:2.
点评 本题考查了新定义的理解和定义域,值域的关系的运用.属于中档题.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
9.命题“?x0∈R,x02-x0>0”的否定是( )
| A. | ?x∈R,x2-x>0 | B. | $?{x_0}∈R,{x_0}^2-{x_0}≤0$ | ||
| C. | ?x∈R,x2-x≤0 | D. | $?{x_0}∈R,{x_0}^2-{x_0}<0$ |
11.已知α是第二象限角,且sinα=$\frac{3}{5}$,则cos(π-α)=( )
| A. | $\frac{4}{5}$ | B. | -$\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | -$\frac{3}{5}$ |
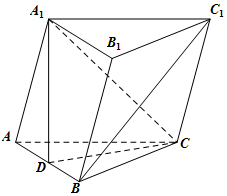 如图,三棱柱ABC-A1B1C1中,AC=BC,AB=AA1,∠A1AB=60°,D是AB的中点.
如图,三棱柱ABC-A1B1C1中,AC=BC,AB=AA1,∠A1AB=60°,D是AB的中点.