题目内容
12.在极坐标系Ox中,曲线C的极坐标方程为p2=$\frac{144}{9+7si{n}^{2}θ}$,以极点O为直角坐标原点、极轴为x轴的正半轴建立平面直角坐标系.(1)求曲线C的直角坐标方程;
(2)设曲线C与x轴、y轴的正半轴分别交于点A、B,P是曲线C上一点,求△ABP面积的最大值.
分析 (Ⅰ)由ρ2=x2+y2,y=ρsinθ,能求出曲线C的直角坐标方程.
(Ⅱ)先求出直线AB的方程,设P(4cosθ,3sinθ),求出P到直线AB的距离,由此能求出△ABP面积的最大值.
解答 解:(Ⅰ)∵曲线C的极坐标方程为ρ2=$\frac{144}{9+7si{n}^{2}θ}$,
∴9ρ2+7ρ2sin2θ=144,
由ρ2=x2+y2,y=ρsinθ,
可得曲线C的直角坐标方程为9x2+9y2+7y2=144.
即曲线C的直角坐标方程为$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{9}=1$.…(5分)
(Ⅱ)∵曲线C与x轴、y轴的正半轴分别交于点A、B,
∴A(4,0),B(0,3),∴直线AB的方程为3x+4y-12=0,
设P(4cosθ,3sinθ),则P到直线AB的距离为:
d=$\frac{|12cosθ+12sinθ-12|}{5}$=$\frac{|12\sqrt{2}sin(θ+\frac{π}{4})-12|}{5}$,
当θ=$\frac{5π}{4}$时,dmax=$\frac{|12\sqrt{2}+12|}{5}$,
∴△ABP面积的最大值为$\frac{1}{2}$×|AB|×$\frac{|12\sqrt{2}+12|}{5}$=6($\sqrt{2}$+1).…(10分)
点评 本题考查曲线的直角坐标方程的求法,考查三角形面积的最大值的求法,是基础题,解题时要认真审题,注意点到直线的距离公式的合理运用.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
7.如图是一个程序框图,则输出的n的值是 ( )
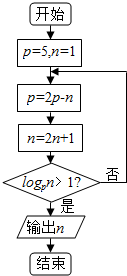

| A. | 29 | B. | 31 | C. | 61 | D. | 63 |
1.抛物线${x^2}=\frac{1}{4}y$的焦点到准线的距离为( )
| A. | 2 | B. | 4 | C. | $\frac{1}{8}$ | D. | $\frac{1}{2}$ |
2.若幂函数y=f(x)的图象经过点($\frac{1}{3}$,3),则该幂函数的解析式为( )
| A. | y=x-1 | B. | y=x${\;}^{\frac{1}{2}}$ | C. | y=x${\;}^{-\frac{1}{3}}$ | D. | y=x3 |