题目内容
9.过椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的右顶点、右焦点的一个圆的圆心(4,y0)在该椭圆上,则y0=$±\frac{12}{5}$.分析 椭圆的右顶点为(5,0),右焦点$(\sqrt{25-{b}^{2}},0)$,由题意可得:$\frac{5+\sqrt{25-{b}^{2}}}{2}$=4,b>0,解得b.把圆心(4,y0)代入椭圆方程即可得出.
解答 解:椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的右顶点为(5,0),右焦点$(\sqrt{25-{b}^{2}},0)$,
由题意可得:$\frac{5+\sqrt{25-{b}^{2}}}{2}$=4,b>0,解得b=4.
∴椭圆的方程为:$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{16}=1$.
∵圆心(4,y0)在该椭圆上,
∴$\frac{{4}^{2}}{25}+\frac{{y}_{0}^{2}}{16}$=1,
解得:y0=$±\frac{12}{5}$.
故答案为:$±\frac{12}{5}$.
点评 本题考查了椭圆的标准方程及其性质、圆的性质、垂直平分线的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
17.若x,y满足约束条件$\left\{\begin{array}{l}{x+2y-2≥0}\\{x-y+3≥0}\\{x≤3}\end{array}\right.$,则z=2x+y的最大值为12.
19.“1,x,16成等比数列”是“x=4”成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
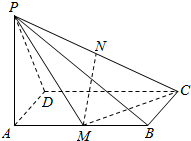 如图,已知PA⊥矩形ABCD所在的平面,M、N分别是AB、PC的中点,若AD=PA=a,AB=$\sqrt{2}$a.
如图,已知PA⊥矩形ABCD所在的平面,M、N分别是AB、PC的中点,若AD=PA=a,AB=$\sqrt{2}$a.