题目内容
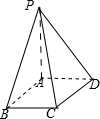
(文科)如图,PA⊥平面ABCD,四边形ABCD为正方形,PA=
,AB=1.
(1)求证:AB⊥平面PAD
(2)求异面直线AB与PC所成角的大小.
| 2 |
(1)求证:AB⊥平面PAD
(2)求异面直线AB与PC所成角的大小.
考点:异面直线及其所成的角,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)根据线面垂直的判定定理即可证明AB⊥平面ABCD;
(2)先找到异面直线所成的角为∠PCD,通过条件求出△PCD的三边长度,根据余弦定理即可求出cos∠PCD,从而求出∠PCD.
(2)先找到异面直线所成的角为∠PCD,通过条件求出△PCD的三边长度,根据余弦定理即可求出cos∠PCD,从而求出∠PCD.
解答:
 解:(1)PA⊥平面ABCD,AD?平面ABCD;
解:(1)PA⊥平面ABCD,AD?平面ABCD;
∴PA⊥AD,即AD⊥PA,又AD⊥AB,PA∩AB=A;
∴AD⊥平面PAB;
(2)PD=
,连接AC,则PC=2,CD=1,∵CD∥AB;
∴∠PCD是异面直线AB与PC所成的角;
∴cos∠PCD=
=
;
∴∠PCD=60°,即异面直线AB与PC所成的角为60°.
 解:(1)PA⊥平面ABCD,AD?平面ABCD;
解:(1)PA⊥平面ABCD,AD?平面ABCD;∴PA⊥AD,即AD⊥PA,又AD⊥AB,PA∩AB=A;
∴AD⊥平面PAB;
(2)PD=
| 3 |
∴∠PCD是异面直线AB与PC所成的角;
∴cos∠PCD=
| 4+1-3 |
| 2×2×1 |
| 1 |
| 2 |
∴∠PCD=60°,即异面直线AB与PC所成的角为60°.
点评:考查线面垂直的性质,线面垂直的判定定理,余弦定理.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目