题目内容
函数f(x)=x3-3ax+b(a≠0).
(1)若曲线y=f(x)在点(2,f(2))处与直线y=8相切,求a,b的值;
(2)求函数f(x)的单调区间与极值点.
(3)若关于x的方程f(x)=b至多有两个零点,求实数b的取值范围.
(1)若曲线y=f(x)在点(2,f(2))处与直线y=8相切,求a,b的值;
(2)求函数f(x)的单调区间与极值点.
(3)若关于x的方程f(x)=b至多有两个零点,求实数b的取值范围.
考点:利用导数研究函数的极值,函数零点的判定定理,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(1)由已知得f′(x)=3x2-3a,且
,由此能求出a,b.
(2)由f′(x)=3(x2-a)(a≠0),利用分类讨论思想和导数性质能求出函数f(x)的单调区间与极值点.
(3)分别求出函数的极大值和极小值,由此能求出实数b的取值范围.
|
(2)由f′(x)=3(x2-a)(a≠0),利用分类讨论思想和导数性质能求出函数f(x)的单调区间与极值点.
(3)分别求出函数的极大值和极小值,由此能求出实数b的取值范围.
解答:
解:(1)∵f(x)=x3-3ax+b(a≠0),
∴f′(x)=3x2-3a,
∵曲线y=f(x)在点(2,f(2))处与直线y=8相切,
∴
,
解得a=4,b=24.
(2)f′(x)=3(x2-a)(a≠0),
当a<0时,f′(x)>0,函数f(x)在(-∞,+∞)上单调递增,
此时函数f(x)没有极值点;
当a>0时,由f′(x)=0,得x=±
,
当x∈(-∞,-
)时,f′(x)>0,函数f(x)单调递增;
当x∈(-
,
)时,f′(x)<0,函数f(x)单调递减;
当x∈(
,+∞)时,f′(x)>0,函数f(x)单调递增,
此时x=-
是f(x)的极大值点,x=
是f(x)的极小值点.
(3)由(2)知,当a>0时,
f(x)极大值=f(-
)=-a
+3a
+b=2a
+b,
f(x)极小值=f(
)=a
-3a
+b=-2a
+b.
∴实数b的取值范围是(-∞,-2a
+b)∪[2a
+b,+∞).
∴f′(x)=3x2-3a,
∵曲线y=f(x)在点(2,f(2))处与直线y=8相切,
∴
|
解得a=4,b=24.
(2)f′(x)=3(x2-a)(a≠0),
当a<0时,f′(x)>0,函数f(x)在(-∞,+∞)上单调递增,
此时函数f(x)没有极值点;
当a>0时,由f′(x)=0,得x=±
| a |
当x∈(-∞,-
| a |
当x∈(-
| a |
| a |
当x∈(
| a |
此时x=-
| a |
| a |
(3)由(2)知,当a>0时,
f(x)极大值=f(-
| a |
| a |
| a |
| a |
f(x)极小值=f(
| a |
| a |
| a |
| a |
∴实数b的取值范围是(-∞,-2a
| a |
| a |
点评:本题主要考查函数、导数等基本知识.考查运算求解能力及化归思想、函数方程思想、分类讨论思想的合理运用,注意导数性质的合理运用.

练习册系列答案
相关题目
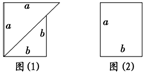 如图所示的两种广告牌,其中图(1)是由两个等腰直角三角形构成的,图(2)是一个矩形,则这两个广告牌面积的大小关系可用含字母a,b(a≠b)的不等式表示为
如图所示的两种广告牌,其中图(1)是由两个等腰直角三角形构成的,图(2)是一个矩形,则这两个广告牌面积的大小关系可用含字母a,b(a≠b)的不等式表示为