题目内容
若函数f(x)=|x|•(x+2)在区间(a,2a+1)上单调递减,则实数a的取值范围是 .
考点:函数单调性的判断与证明
专题:函数的性质及应用
分析:根据分段函数的性质,求出函数f(x)的单调递减区间,解不等式即可得到结论.
解答:
解:当x≥0时,f(x)=|x|•(x+2)=x•(x+2)=(x+1)2-1,函数在[0,+∞)上单调递增,
当x<0时,f(x)=|x|•(x+2)=-x•(x+2)=-(x+1)2+1,函数在[-1,0)上递减,在(-∞,-1)上递增,
若在区间(a,2a+1)上单调递减,
则
,即
,
则-1≤a≤-
,
故答案为:(-1,-
]
当x<0时,f(x)=|x|•(x+2)=-x•(x+2)=-(x+1)2+1,函数在[-1,0)上递减,在(-∞,-1)上递增,
若在区间(a,2a+1)上单调递减,
则
|
|
则-1≤a≤-
| 1 |
| 2 |
故答案为:(-1,-
| 1 |
| 2 |
点评:本题主要考查函数单调区间的应用,根据分段函数的性质求出递减区间时解决本题的关键.

练习册系列答案
相关题目
已知函数f(x)=x2•cos(xπ),若an=f(n)+f(n+1),则
ai=( )
| 2014 |
 |
| i=1 |
| A、-2015 | B、-2014 |
| C、2014 | D、2015 |
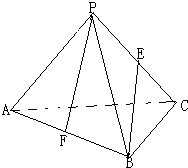 如图,在正四面体PABC中,若E,F分别是PC,AB的中点,则异面直线PF与BE所成的角的余弦值为
如图,在正四面体PABC中,若E,F分别是PC,AB的中点,则异面直线PF与BE所成的角的余弦值为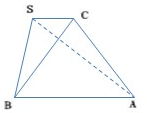 已知在三棱锥S-ABC中,△SBC、△ABC都是等边三角形,平面SBC⊥平面ABC,SA=6,则三棱锥体积为
已知在三棱锥S-ABC中,△SBC、△ABC都是等边三角形,平面SBC⊥平面ABC,SA=6,则三棱锥体积为