题目内容
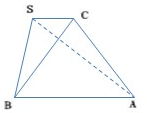 已知在三棱锥S-ABC中,△SBC、△ABC都是等边三角形,平面SBC⊥平面ABC,SA=6,则三棱锥体积为
已知在三棱锥S-ABC中,△SBC、△ABC都是等边三角形,平面SBC⊥平面ABC,SA=6,则三棱锥体积为考点:棱柱、棱锥、棱台的体积
专题:综合题,空间位置关系与距离
分析:取BC的中点D,连接SD,AD,证明SD⊥平面ABC,再求三棱锥体积.
解答:
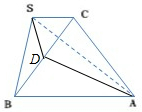 解:取BC的中点D,连接SD,AD
解:取BC的中点D,连接SD,AD
∵△SBC、△ABC都是等边三角形,
∴SB=SC=AB=AC=BC,而D∈BC且BD=CD,
∴BC⊥SD、BC⊥AD,
又平面SBC⊥平面ABC,
∴SD⊥平面ABC,
∴SD⊥AD,
∴SD=AD=3
,
∵SB=SC=AB=AC、D∈BC且BD=CD,
∴BC=2
.
∴S△ABC=
BC×AD=
×2
×3
=6
.
∴VS-ABC=
×6
×3
=6
.
故答案为:6
.
 解:取BC的中点D,连接SD,AD
解:取BC的中点D,连接SD,AD∵△SBC、△ABC都是等边三角形,
∴SB=SC=AB=AC=BC,而D∈BC且BD=CD,
∴BC⊥SD、BC⊥AD,
又平面SBC⊥平面ABC,
∴SD⊥平面ABC,
∴SD⊥AD,
∴SD=AD=3
| 2 |
∵SB=SC=AB=AC、D∈BC且BD=CD,
∴BC=2
| 6 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 6 |
| 2 |
| 3 |
∴VS-ABC=
| 1 |
| 3 |
| 3 |
| 2 |
| 6 |
故答案为:6
| 6 |
点评:本题考查三棱锥体积的计算,证明SD⊥平面ABC是关键.

练习册系列答案
相关题目
已知双曲线
-
=1(a>0,b>0)以及双曲线
-
=1(a>0,b>0)的渐近线将第一象限三等分,则双曲线
-
=1的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| y2 |
| a2 |
| x2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
A、2或
| ||||||
B、
| ||||||
C、
| ||||||
D、2或
|