题目内容
已知cosx=
,x∈(-
,0),则
= .
| 3 |
| 5 |
| π |
| 2 |
|
考点:二阶矩阵,三角函数中的恒等变换应用
专题:矩阵和变换
分析:由cosx=
,x∈(-
,0),得sinx=-
,再由
=sinx-cosx,能求出结果.
| 3 |
| 5 |
| π |
| 2 |
| 4 |
| 5 |
|
解答:
解:∵cosx=
,x∈(-
,0),
∴sinx=-
,
∴
=sinx-cosx=-
-
=-
.
故答案为:-
.
| 3 |
| 5 |
| π |
| 2 |
∴sinx=-
| 4 |
| 5 |
∴
|
| 4 |
| 5 |
| 3 |
| 5 |
| 7 |
| 5 |
故答案为:-
| 7 |
| 5 |
点评:本题考查二阶矩阵的求法,是基础题,解题时要认真审题,注意三角函数的性质的灵活运用.

练习册系列答案
相关题目
某算法的程序框图如图所示,则输出的S的值为( )


A、
| ||
B、
| ||
C、
| ||
D、
|
为了得到函数y=sin(3x+1),x∈R的图象,只需将函数y=sin3x,x∈R的图象( )
| A、向左平移1个的单位长度 | ||
| B、向右平移1个的单位长度 | ||
C、向左平移
| ||
D、向右平移
|
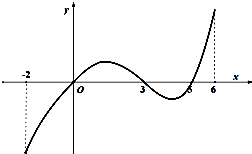 已知函数f(x)的定义域为[-2,6],x与f(x)部分对应值如下表,
已知函数f(x)的定义域为[-2,6],x与f(x)部分对应值如下表,