题目内容
对正整数n,设曲线y=xn(1-x)在x=2处的切线与y轴交点的纵坐标为an,则数列 的前n项和是________.
的前n项和是________.
2n+1-2
[解析] ∵y=xn(1-x),∴y′=(xn)′(1-x)+(1-x)′·xn=n·xn-1(1-x)-xn.
f ′(2)=-n·2n-1-2n=(-n-2)·2n-1.
在点x=2处点的纵坐标为y=-2n.
∴切线方程为y+2n=(-n-2)·2n-1(x-2).
令x=0得,y=(n+1)·2n,
∴an=(n+1)·2n,
∴数列 的前n项和为
的前n项和为 =2n+1-2.
=2n+1-2.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
 an,则数列的通项公式an=________.
an,则数列的通项公式an=________. ;
;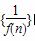 的前n项和为Sn,则S2014的值为( )
的前n项和为Sn,则S2014的值为( )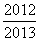 B.
B. C.
C.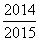 D.
D.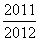
 (k为常数,e=2.71828…是自然对数的底数),曲线y=f(x)在点(1,f(1))处的切线与x轴平行.
(k为常数,e=2.71828…是自然对数的底数),曲线y=f(x)在点(1,f(1))处的切线与x轴平行.