题目内容
8.关于x的不等式|$|\begin{array}{l}{x+a}&{2}\\{1}&{x}\end{array}|$<0的解集为(-1,b).(1)求实数a,b的值;
(2)若z1=a+bi,z2=cosα+isinα,且z1z2为纯虚数,求tanα的值.
分析 (1)由题意可得:-1,b是方程x2+ax-2=0的两个实数根,利用根与系数的关系即可得出.
(2)z1z2=(-cosα-2sinα)+(2cosα-sinα)i为纯虚数,利用纯虚数的定义即可得出.
解答 解:(1)不等式|$|\begin{array}{l}{x+a}&{2}\\{1}&{x}\end{array}|$<0即x(x+a)-2<0的解集为(-1,b).
∴-1,b是方程x2+ax-2=0的两个实数根,∴-1+b=-a,-b=-2,
解得a=-1,b=2.
(2)z1z2=(-1+2i)(cosα+isinα)=(-cosα-2sinα)+(2cosα-sinα)i为纯虚数,
∴-cosα-2sinα=0,2cosα-sinα≠0,
解得tanα=-$\frac{1}{2}$.
点评 本题考查了复数的运算法则、纯虚数的定义、一元二次方程的根与系数的关系、一元二次不等式的解法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
3.已知$\overrightarrow a=(1,-2)$,$\overrightarrow b=(2,m)$,若$\overrightarrow a⊥\overrightarrow b$,则$|\overrightarrow b|$=( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
13.已知集合A={0,a,a2},且1∈A,则a=( )
| A. | 1 | B. | -1 | C. | ±1 | D. | 0 |
17.数列{an}是等差数列,且a1>0,若a1008+a1009>0,a1008•a1009<0同时成立,则使得Sn>0成立的n的最大值为( )
| A. | 2016 | B. | 2017 | C. | 2018 | D. | 2019 |
18.如图是一个算法的程序框图,当输入x的值为3时,输出y的结果恰好是$\frac{1}{3}$,则?处的关系式可以是( )
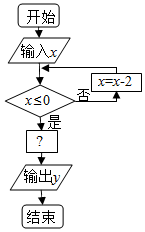

| A. | y=x2 | B. | y=3-x | C. | y=3x | D. | y=x${\;}^{\frac{1}{3}}$ |