题目内容
已知正三棱锥P-ABC,点P,A,B,C都在半径为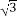 的球面上,若PA,PB,PC两两互相垂直,则球心到截面ABC的距离为____________.
的球面上,若PA,PB,PC两两互相垂直,则球心到截面ABC的距离为____________.

【解析】
试题分析:先利用正三棱锥的特点,将球的内接三棱锥问题转化为球的内接正方体问题,从而将所求距离转化为正方体中,中心到截面的距离问题,利用等体积法可实现此计算.
∵正三棱锥P-ABC,PA,PB,PC两两垂直,∴此正三棱锥的外接球即以PA,PB,PC为三边的正方体的外接球O,∵球O的半径为 , ∴正方体的边长为2,即PA=PB=PC=2,球心到截面ABC的距离即正方体中心到截面ABC的距离,设P到截面ABC的距离为h,则正三棱锥P-ABC的体积
, ∴正方体的边长为2,即PA=PB=PC=2,球心到截面ABC的距离即正方体中心到截面ABC的距离,设P到截面ABC的距离为h,则正三棱锥P-ABC的体积
△ABC为边长为 的正三角形,
的正三角形, ∴球心(即正方体中心)O到截面ABC的距离为
∴球心(即正方体中心)O到截面ABC的距离为
考点:球的内接多面体,棱锥的结构特征

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 若关于x的方程
若关于x的方程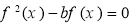 恰有三个不同的实数解,则实数b的取值范围是( ).
恰有三个不同的实数解,则实数b的取值范围是( ).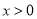 ,则“
,则“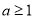 ”是“
”是“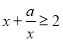 恒成立”的( )
恒成立”的( )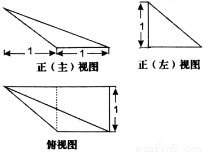
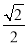 B.
B.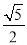 C.
C.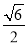 D.
D.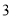
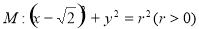 ,若椭圆
,若椭圆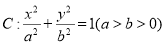 的右顶点为圆
的右顶点为圆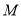 的圆心,离心率为
的圆心,离心率为 .
.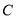 的方程;
的方程;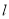 与椭圆
与椭圆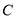 分别交于
分别交于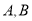 两点,与圆
两点,与圆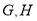 两点,点
两点,点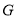 在线段AB上,且
在线段AB上,且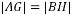 ,求圆M的半径r的取值范围.
,求圆M的半径r的取值范围. 为
为 的导函数,则
的导函数,则 的图像是( )
的图像是( ) B.
B. C.
C. D.
D.

 B.
B.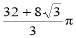
 D.
D.
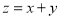 ,其中实数
,其中实数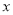 ,
,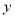 满足
满足 ,则
,则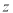 的最大值为( )
的最大值为( )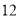 B.
B.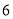 C.
C.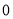 D.
D.
 ,若
,若 的最小值为
的最小值为 B.8 C.
B.8 C. D.
D.