题目内容
已知|
|=4,|
|=3,(2
-3
)•(2
+
)=61.
①
与
的夹角;
②求|
+
|和|
-
|.
| a |
| b |
| a |
| b |
| a |
| b |
①
| a |
| b |
②求|
| a |
| b |
| a |
| b |
考点:数量积表示两个向量的夹角,向量的模
专题:平面向量及应用
分析:(1)根据平面向量的数量积求出夹角θ;
(2)由
•
的值,以及|
|与|
|的值,求出|
+
|与|
-
|的值.
(2)由
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
解答:
解:(1)∵|
|=4,|
|=3,
∴(2
-3
)•(2
+
)=4
2-4
•
-3
2=61,
∴64-4
•
-27=61,
即-4
•
=24,
∴
•
=-6;
∴cosθ=
=
=-
,
∴θ=120°;
(2)∵
•
=-6,
∴|
+
|=
=
=
;
|
-
|=
=
=
.
| a |
| b |
∴(2
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| b |
∴64-4
| a |
| b |
即-4
| a |
| b |
∴
| a |
| b |
∴cosθ=
| ||||
|
|
| -6 |
| 4×3 |
| 1 |
| 2 |
∴θ=120°;
(2)∵
| a |
| b |
∴|
| a |
| b |
|
=
| 16-2×6+9 |
=
| 13 |
|
| a |
| b |
|
=
| 16+2×6+9 |
=
| 37 |
点评:本题考查了平面向量的数量积的应用问题,解题时应利用数量积求两向量的夹角与模长,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
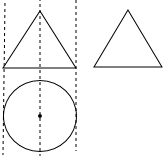 如图,一个空间几何体的正视图和左视图都是边长为1的正三角形,俯视图是一个圆,那么这个几何体的内切球表面积为( )
如图,一个空间几何体的正视图和左视图都是边长为1的正三角形,俯视图是一个圆,那么这个几何体的内切球表面积为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
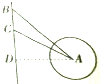 某学校组织同学们参加红色七日游---海上夏令营活动,如图,海中小岛A周围20海里内有暗礁,夏令营的船只船向正南航行,在B处测得小岛A在船的南偏东30°,船行30海里后,在C处测得小岛A在船的南偏东45°,如果此船不改变航向,继续向南航行,有无触礁的危险?
某学校组织同学们参加红色七日游---海上夏令营活动,如图,海中小岛A周围20海里内有暗礁,夏令营的船只船向正南航行,在B处测得小岛A在船的南偏东30°,船行30海里后,在C处测得小岛A在船的南偏东45°,如果此船不改变航向,继续向南航行,有无触礁的危险?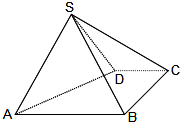 如图,四棱锥S-ABCD中,AB∥CD,BC⊥CD,侧面SAB为等边三角形.AB=BC=2,CD=1,SD=
如图,四棱锥S-ABCD中,AB∥CD,BC⊥CD,侧面SAB为等边三角形.AB=BC=2,CD=1,SD=