题目内容
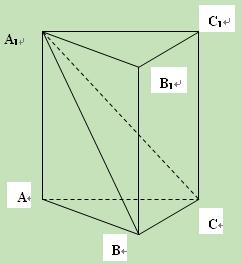
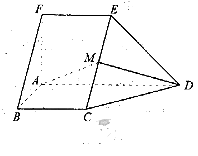
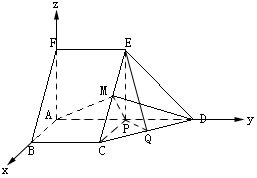
如图,在五面体ABCDEF中,FA 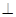 平面ABCD, AD//BC//FE,AB
平面ABCD, AD//BC//FE,AB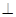 AD,M为EC的中点,AF=AB=BC=FE=
AD,M为EC的中点,AF=AB=BC=FE=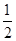 AD
AD
(1)求异面直线BF与DE所成的角的大小;
(2)证明平面 AMD
AMD 平面CDE;
平面CDE;
(3)求二面角A-CD- E的余弦值.
E的余弦值.
 平面ABCD, AD//BC//FE,AB
平面ABCD, AD//BC//FE,AB AD,M为EC的中点,AF=AB=BC=FE=
AD,M为EC的中点,AF=AB=BC=FE=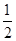 AD
AD(1)求异面直线BF与DE所成的角的大小;
(2)证明平面
 AMD
AMD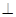 平面CDE;
平面CDE;(3)求二面角A-CD-
 E的余弦值.
E的余弦值.
(1)BC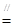 FE ……………………1分
FE ……………………1分
∴BCEF是□ ∴BF//CE
∴∠CED或其补角为BF与DE所成角 ………………… …2分
…2分
取 AD中点P连结EP和CP
AD中点P连结EP和CP
∵ FE
FE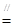 AP ∴FA
AP ∴FA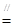 EP
EP
同理AB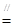 PC 又FA⊥平面ABCD ∴EF⊥平面ABCD
PC 又FA⊥平面ABCD ∴EF⊥平面ABCD
∴EP⊥PC、EP⊥AD 由AB⊥AD PC⊥AD
设FA=a,则EP=PC=PD=a
CD=DE=EC=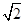 a ∴△ECD是正三角形 ∴∠CED=60o
a ∴△ECD是正三角形 ∴∠CED=60o
∴BF与DE成角60o ……………………2分
(2)∵DC=DE,M为EC中点 ∴DM⊥EC
连结MP,则MP⊥CE 又DM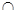 MP=M
MP=M
∴DE⊥平面ADM ……………………3分
又CE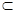 平面CDE ∴平面AMD⊥平面CDE …… ………1分
平面CDE ∴平面AMD⊥平面CDE …… ………1分
( 3)取CD中点Q,连结PQ和EQ ∵PC=DQ
3)取CD中点Q,连结PQ和EQ ∵PC=DQ
∴PQ⊥CD,同理EQ⊥CD ∴∠PQE为二面角的平面角 ……………2分
在Rt△EPQ中,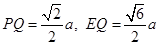
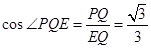
∴二面角A-CD-E的余弦值为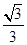
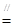 FE ……………………1分
FE ……………………1分∴BCEF是□ ∴BF//CE
∴∠CED或其补角为BF与DE所成角 …………………
 …2分
…2分取
 AD中点P连结EP和CP
AD中点P连结EP和CP
∵
 FE
FE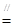 AP ∴FA
AP ∴FA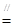 EP
EP同理AB
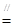 PC 又FA⊥平面ABCD ∴EF⊥平面ABCD
PC 又FA⊥平面ABCD ∴EF⊥平面ABCD∴EP⊥PC、EP⊥AD 由AB⊥AD PC⊥AD
设FA=a,则EP=PC=PD=a
CD=DE=EC=
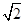 a ∴△ECD是正三角形 ∴∠CED=60o
a ∴△ECD是正三角形 ∴∠CED=60o∴BF与DE成角60o ……………………2分
(2)∵DC=DE,M为EC中点 ∴DM⊥EC
连结MP,则MP⊥CE 又DM
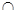 MP=M
MP=M∴DE⊥平面ADM ……………………3分
又CE
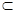 平面CDE ∴平面AMD⊥平面CDE …… ………1分
平面CDE ∴平面AMD⊥平面CDE …… ………1分(
 3)取CD中点Q,连结PQ和EQ ∵PC=DQ
3)取CD中点Q,连结PQ和EQ ∵PC=DQ∴PQ⊥CD,同理EQ⊥CD ∴∠PQE为二面角的平面角 ……………2分
在Rt△EPQ中,
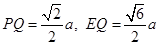
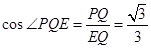
∴二面角A-CD-E的余弦值为
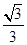
略

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
 =
=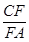 =
=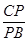 =
= (如图(1)),将△AEF沿EF折起到△
(如图(1)),将△AEF沿EF折起到△ EF的位置,使二面角
EF的位置,使二面角 EF
EF
 中,
中,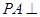 面
面 ,
, ,
, ,
, 为
为 上一点,
上一点, ,
,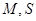 分别为
分别为 的中点.
的中点. 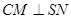 .
. 与面
与面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值. (包括端点)上是否存在一点
(包括端点)上是否存在一点 ,使
,使 平面
平面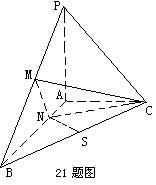
 中, AB=1,
中, AB=1, ,
, .
. ;
; —B的余弦值。
—B的余弦值。
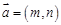 ,
,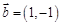 ,其中
,其中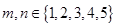 ,则
,则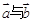 的夹角能成为直角三角形内角的概率是
的夹角能成为直角三角形内角的概率是  ,
, ,
, ,且
,且 ,则
,则 .
. 关于
关于 轴的对称点是B
轴的对称点是B ,则
,则 的值依次是( )
的值依次是( )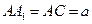 ,直线AC与平面A1BC所成的角为
,直线AC与平面A1BC所成的角为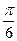 ,
,