题目内容
6.解不等式:(1)$\frac{3x-2}{2x}≥1$;(2)$\frac{{x}^{2}-x-2}{{x}^{2}+5x+6}<0$.分析 (1)$\frac{3x-2}{2x}≥1$移项,通分,利用同号得正求解即可或者转化为二次不等式的解法;
(2)分子分母因式分解,利用标根法求解即可.
解答 解::(1)$\frac{3x-2}{2x}≥1$;
可得:$\frac{3x-2}{2x}-1≥0$;即$\frac{x-2}{2x}≥0$,
∴2x(x-2)≥0,且x≠0.
解得:x≥2或x<0,
∴原不等式的解集为{x|x≥2或x<0}.
(2)$\frac{{x}^{2}-x-2}{{x}^{2}+5x+6}<0$.
原不等式化简为:$\frac{(x-2)(x+1)}{(x+2)(x+3)}<0$,
转化为整数不等式:(x+3)(x+2)(x+1)(x-2)<0.
令:x+3)(x+2)(x+1)(x-2)=0.
可得方程的根x1=-3,x2=-2,x3=-1,x4=2.
标根穿线:小于0,取下部分.分母不能取等.
∴原不等式的解集为{x|2>x>-1或-3<x<-2}.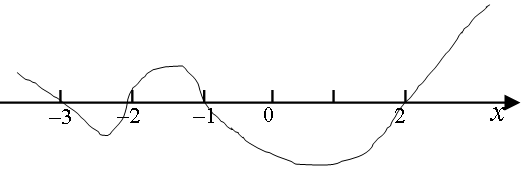
点评 本题考查不等式的解法,主要考查高次不等式的解法注意转化为整式不等式,考查运算能力,属于基础题.

练习册系列答案
相关题目
17.已知集合A={x∈Z|x2-16<0},B={x|x2-4x+3>0},则A∩B=( )
| A. | {x|-4<x<1或3<x<4} | B. | {-4,-3,-2,-1,0,3,4} | ||
| C. | {x|x<1或3<x<4} | D. | {-3,-2,-1,0} |
11.已知多面体ABCDFE的每个顶点都在球O的表面上,四边形ABCD为正方形,EF∥BD,且E,F在平面ABCD内的射影分别为B,D,若△ABE的面积为2,则球O的表面积的最小值为( )
| A. | 8$\sqrt{2}$π | B. | 8π | C. | 12$\sqrt{2}$π | D. | 12π |
1.已知数列{an}满足a1=1,且对任意的正整数n,有an+1=2an成立,则a3a5=( )
| A. | $\frac{1}{64}$ | B. | 32 | C. | 64 | D. | $\frac{1}{32}$ |
 一直升飞机的航线和山顶在同一铅垂平面内,已知飞机的高度为海拔20000m,速度为170($\sqrt{3}$+1)km/h,飞行员在A处看到山顶的俯角为30°,经过360秒后到B处又看到山顶的俯角为135°,求山顶的海拔高度.
一直升飞机的航线和山顶在同一铅垂平面内,已知飞机的高度为海拔20000m,速度为170($\sqrt{3}$+1)km/h,飞行员在A处看到山顶的俯角为30°,经过360秒后到B处又看到山顶的俯角为135°,求山顶的海拔高度. 如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点.
如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点.