题目内容
14.已知点F(1,0),直线l:x=-1,直线l′垂直l于点P,线段PF的垂直平分线交直线l′于点Q.(Ⅰ)求点Q的轨迹C的方程;
(Ⅱ)已知轨迹C上的不同两点M,N与P(1,2)的连线的斜率之和为2,求证:直线MN过定点.
分析 (Ⅰ)由题意画出图形,可得点Q的轨迹是以F为焦点,l为准线的抛物线,则点Q的轨迹C的方程可求;
(Ⅱ)设直线MN的方程为x=my+a,联立直线方程与抛物线方程,写出MP、NP所在直线的斜率,结合根与系数的关系求得a值,可得直线MN过定点.
解答 (Ⅰ)解:依题意得|QP|=|QF|,即Q到直线l:x=-1的距离与到点F的距离相等,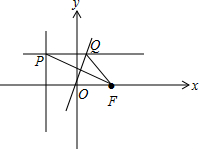
∴点Q的轨迹是以F为焦点,l为准线的抛物线.
设抛物线方程为y2=2px(p>0),则p=2,
即点Q的轨迹C的方程是y2=4x;
(Ⅱ)证明:设直线MN的方程为x=my+a,M(x1,y1),N(x2,y2),
由$\left\{\begin{array}{l}{{y}^{2}=4x}\\{x=my+a}\end{array}\right.$,得y2-4my-4a=0.
∴y1y2=-4a,
kMP=$\frac{{y}_{1}-2}{{x}_{1}-1}$=$\frac{{y}_{1}-2}{\frac{{{y}_{1}}^{2}}{4}-1}$=$\frac{4}{{y}_{1}+2}$,同理得kNP=$\frac{4}{{y}_{2}+2}$,
∴$\frac{4}{{y}_{1}+2}$+$\frac{4}{{y}_{2}+2}$=2.
化简得:y1y2=4,
又y1y2=-4a,∴a=-1,
∴直线MN过定点(-1,0).
点评 本题考查轨迹方程的求法,考查直线与抛物线位置关系的应用,考查灵活运算能力,是中档题.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
4.若对于任意的实数t,函数f(x)=(x-t)3+(x-et)3-3ax在R上都是增函数,则实数a的取值范围是( )
| A. | (-$∞,\frac{1}{2}$] | B. | ($-∞,\frac{1}{2}$) | C. | ($-∞,\frac{\sqrt{2}}{2}$] | D. | ($-∞,\frac{\sqrt{2}}{2}$) |
2. 执行如图所示的程序框图,则输出的s值为( )
执行如图所示的程序框图,则输出的s值为( )
 执行如图所示的程序框图,则输出的s值为( )
执行如图所示的程序框图,则输出的s值为( )| A. | -$\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | 2 | D. | 3 |