题目内容
19.已知a=(1-i)(1+bi),其中a,b是实数,i是虚数单位,则$\frac{a+bi}{i}$=( )| A. | 2+i | B. | 1+2i | C. | 2-i | D. | 1-2i |
分析 根据题意,利用复数相等列出方程组,求出a、b的值,再计算$\frac{a+bi}{i}$的值.
解答 解:∵a=(1-i)(1+bi)=(1+b)+(b-1)i,
且a,b是实数,i是虚数单位,
∴$\left\{\begin{array}{l}{a=1+b}\\{0=b-1}\end{array}\right.$,
解得a=2,b=1;
∴$\frac{a+bi}{i}$=$\frac{2+i}{i}$=$\frac{(2+i)i}{{i}^{2}}$=1-2i.
故选:D.
点评 本题考查了复数的概念与代数形式的运算问题,是基础题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.已知函数f(x)=-8sinx+tanx(x∈($-\frac{π}{2}$,$\frac{π}{2}$)),则f(x)为增函数的概率为( )
| A. | $\frac{2}{π}$ | B. | $\frac{1}{π}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
14.方程C${\;}_{16}^{{x}^{2}-x}$=C${\;}_{16}^{5x-5}$的解集是( )
| A. | {1,3,5,7} | B. | {1,3,5} | C. | {3,5} | D. | {1,3} |
11.已知复数z的共轭复数$\overline{z}$,且$\overline{z}=\frac{z}{1+i}$+2(i为虚数单位),则z在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |

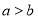 ,二次三项式
,二次三项式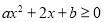 对于一切实数
对于一切实数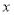 恒成立,又
恒成立,又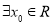 ,使
,使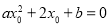 成立,则
成立,则 的最小值为( )
的最小值为( )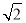 C.2 D.
C.2 D.