题目内容
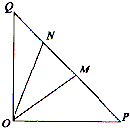 如图,在等腰直角三角形△OPQ中,∠OPQ=90°,OP=2
如图,在等腰直角三角形△OPQ中,∠OPQ=90°,OP=2| 2 |
(1)若OM=
| 5 |
(2)若点N在线段MQ上,且∠MON=30°,问:当∠POM取何值时,△OMN的面积最小?并求出面积的最小值.
分析:(1)在△OPQ中,由余弦定理得,OM2=OP2+MP2-2•OP•MPcos45°,解得MP即可.
(2)∠POM=α,0°≤α≤60°,在△OMP中,由正弦定理求出OM,同理求出ON,推出三角形的面积,利用两角和与差的三角函数化简面积的表达式,通过α的范围求出面积的最大值.
(2)∠POM=α,0°≤α≤60°,在△OMP中,由正弦定理求出OM,同理求出ON,推出三角形的面积,利用两角和与差的三角函数化简面积的表达式,通过α的范围求出面积的最大值.
解答:解:(1)在△OPQ中,∠OPQ=45°,OM=
,OP=2
,
由余弦定理得,OM2=OP2+MP2-2•OP•MPcos45°,
得MP2-4MP+3=0,解得MP=1或MP=3.…6
(2)设∠POM=α,0°≤α≤60°,
在△OMP中,由正弦定理,得
=
,
所以OM=
,同理ON=
…8′
S△OMN=
×OM×ON×sin∠MON=
×
…10
=
=
═
=
=
…14
因为0°≤α≤60°,30°≤2α+30°≤150°,
所以当α=30°时,sin(2α+30°)的最大值为1,
此时△OMN的面积取到最小值.
即∠POM=30°时,△OMN的面积的最小值为8-4
.…16
| 5 |
| 2 |
由余弦定理得,OM2=OP2+MP2-2•OP•MPcos45°,
得MP2-4MP+3=0,解得MP=1或MP=3.…6
(2)设∠POM=α,0°≤α≤60°,
在△OMP中,由正弦定理,得
| OM |
| sin∠OPM |
| OP |
| sin∠OMP |
所以OM=
| OPsin45° |
| sin(45°+α) |
| OPsin45° |
| sin(75°+α) |
S△OMN=
| 1 |
| 2 |
| 1 |
| 4 |
| OP2sin245° |
| sin(45°+α)sin(75°+α) |
=
| 1 |
| sin(45°+α)sin(75°+α) |
| 1 | ||||||
sin(45°+α)[
|
═
| 1 | ||||||
|
=
| 1 | ||||||||||
|
| 1 | ||||||
|
因为0°≤α≤60°,30°≤2α+30°≤150°,
所以当α=30°时,sin(2α+30°)的最大值为1,
此时△OMN的面积取到最小值.
即∠POM=30°时,△OMN的面积的最小值为8-4
| 3 |
点评:本题考查正弦定理以及余弦定理两角和与差的三角函数的应用,考查转化思想以及计算能力.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
 如图,在等腰直角三角形ABC中,AC=BC=1,点M,N分别是AB,BC的中点,点P是△ABC(包括边界)内任一点.则
如图,在等腰直角三角形ABC中,AC=BC=1,点M,N分别是AB,BC的中点,点P是△ABC(包括边界)内任一点.则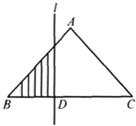 如图,在等腰直角三角形ABC中,BC=4,当一条垂直于底边BC(垂足为D)的直线l从左至右移动(与直角三角形ABC有公共点)时,直线l把直角三角形分成两部分,令BD=x,试写出图中阴影部分的面积y与x的函数关系式.
如图,在等腰直角三角形ABC中,BC=4,当一条垂直于底边BC(垂足为D)的直线l从左至右移动(与直角三角形ABC有公共点)时,直线l把直角三角形分成两部分,令BD=x,试写出图中阴影部分的面积y与x的函数关系式. 如图,在等腰直角三角形ABC中,则AM<AC的概率为( )
如图,在等腰直角三角形ABC中,则AM<AC的概率为( )
 如图,在等腰直角三角形ABC中,AC=BC=1,点M,N分别是AB,BC的中点,点P是△ABC(包括边界)内任一点.则
如图,在等腰直角三角形ABC中,AC=BC=1,点M,N分别是AB,BC的中点,点P是△ABC(包括边界)内任一点.则