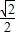题目内容
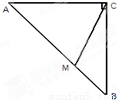
 如图,在等腰直角三角形ABC中,AC=BC=1,点M,N分别是AB,BC的中点,点P是△ABC(包括边界)内任一点.则
如图,在等腰直角三角形ABC中,AC=BC=1,点M,N分别是AB,BC的中点,点P是△ABC(包括边界)内任一点.则| AN |
| MP |
分析:选择合适的原点建立坐标系,分别给出动点(含参数)和定点的坐标,结合向量内积计算公式进行求解.
解答:解:以C为坐标原点,CA边所在直线为x轴,建立直角坐标系,
则A(1,0),B(0,1),
设P(x,y),
则
且
=(-1,
),
=(x-
,y-
)
•
=-x+
y+
,
令t=-x+
y+
,结合线性规划知识,
则y=2x+2t-
当直线t=-x+
y+
经过点A(1,0)时,
•
有最小值,
将(1,0)代入得t=-
,
当直线t=-x+
y+
经过点B时,
•
有最大值,
将(0,1)代入得t=
,
故答案为[-
,
].
则A(1,0),B(0,1),
设P(x,y),
则
|
且
| AN |
| 1 |
| 2 |
| MP |
| 1 |
| 2 |
| 1 |
| 2 |
| AN |
| MP |
| 1 |
| 2 |
| 1 |
| 4 |
令t=-x+
| 1 |
| 2 |
| 1 |
| 4 |
则y=2x+2t-
| 1 |
| 2 |
当直线t=-x+
| 1 |
| 2 |
| 1 |
| 4 |
| AN |
| MP |
将(1,0)代入得t=-
| 3 |
| 4 |
当直线t=-x+
| 1 |
| 2 |
| 1 |
| 4 |
| AN |
| MP |
将(0,1)代入得t=
| 3 |
| 4 |
故答案为[-
| 3 |
| 4 |
| 3 |
| 4 |
点评:本题考查的知识点是平面向量的数量积运算及线性规划,处理的关键是建立恰当的坐标系,求出各点、向量的坐标,利用平面向量的数量积公式,将其转化为线性规划问题,再利用“角点法”解决问题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
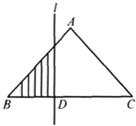 如图,在等腰直角三角形ABC中,BC=4,当一条垂直于底边BC(垂足为D)的直线l从左至右移动(与直角三角形ABC有公共点)时,直线l把直角三角形分成两部分,令BD=x,试写出图中阴影部分的面积y与x的函数关系式.
如图,在等腰直角三角形ABC中,BC=4,当一条垂直于底边BC(垂足为D)的直线l从左至右移动(与直角三角形ABC有公共点)时,直线l把直角三角形分成两部分,令BD=x,试写出图中阴影部分的面积y与x的函数关系式. 如图,在等腰直角三角形ABC中,则AM<AC的概率为( )
如图,在等腰直角三角形ABC中,则AM<AC的概率为( )