题目内容
已知函数f(x)=x3+3xf′(0)-2ex则f′(1)等于 .
考点:导数的运算
专题:导数的概念及应用
分析:求函数的导数,让x=0,建立关于f′(0)的方程,解出f'(x),代入x=1即可求解.
解答:
解:∵f(x)=x3+3xf′(0)-2ex,
∴f'(x)=3x2+3f′(0)-2ex,
∴f'(0)=3f′(0)-2,
解得,f'(0)=1.
∴f'(x)=3x2+3-2ex,
∴f′(1)=9-2e2.
故答案为:9-2e2.
∴f'(x)=3x2+3f′(0)-2ex,
∴f'(0)=3f′(0)-2,
解得,f'(0)=1.
∴f'(x)=3x2+3-2ex,
∴f′(1)=9-2e2.
故答案为:9-2e2.
点评:本题主要考查导数的计算和求值,利用f′(0)为常数,建立关于f′(0)的方程是解决本题的关键,比较基础.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
奇函数f(x)=
(其中a为常数)的定义域为( )
| ||
| x-a |
| A、(-1,0)∪(0,1) |
| B、[-1,0)∪(0,-1] |
| C、[-1,1] |
| D、(-∞,-1][1,+∞) |
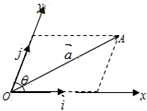 已知单位向量
已知单位向量