题目内容
9.已知在△ABC中,∠A=60°,D为AC上一点,且BD=3,$\overrightarrow{AC}$•$\overrightarrow{AD}$=$\overrightarrow{AC}$•$\overrightarrow{AB}$,则$\overrightarrow{AD}$•$\overrightarrow{AB}$等于( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 可画出图形,设A,B,C所对的边分别为a,b,c,并设AD=m,这样根据便可得到$bm=\frac{bc}{2}$,从而得到m=$\frac{c}{2}$,这样在△ABD中由余弦定理便可建立关于c的方程,可解出c=$2\sqrt{3}$,从而有m=$\sqrt{3}$,然后进行数量积的计算便可求出$\overrightarrow{AD}•\overrightarrow{AB}$的值.
解答 解:如图,设△ABC的内角A,B,C所对的边分别为a,b,c,且设AD=m;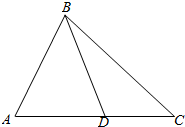
∵∠A=60°,∴由$\overrightarrow{AC}•\overrightarrow{AD}=\overrightarrow{AC}•\overrightarrow{AB}$得:$bm=\frac{bc}{2}$;
∴$m=\frac{c}{2}$;
又BD=3,∴在△ABD中由余弦定理得:
$9=\frac{{c}^{2}}{4}+{c}^{2}-\frac{{c}^{2}}{2}$;
∴$c=2\sqrt{3}$,m=$\sqrt{3}$;
∴$\overrightarrow{AD}•\overrightarrow{AB}=mc•cos60°=\sqrt{3}•2\sqrt{3}•\frac{1}{2}=3$.
故选:C.
点评 考查向量数量积的计算公式,余弦定理,以及向量夹角的概念.

练习册系列答案
相关题目
19.若角α∈(-π,-$\frac{π}{2}$),则$\sqrt{\frac{1+sinα}{1-sinα}}$-$\sqrt{\frac{1-sinα}{1+sinα}}$=( )
| A. | -2tanα | B. | 2tanα | C. | -tanα | D. | tanα |
20.过点P(-2,m)和Q(m,4)的直线斜率等于1,那么m的值等于( )
| A. | 1或3 | B. | 4 | C. | 1 | D. | 1或4 |
1.已知圆C过点$A(2,0),B(0,2\sqrt{2})$,且圆心C在直线y=0上,则圆C的方程为( )
| A. | (x-1)2+y2=9 | B. | (x-2)2+y2=16 | C. | (x+1)2+y2=9 | D. | (x+2)2+y2=16 |
19.《中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在20~80mg/100ml(不含80)之间,属于酒后驾车;在80mg/100ml(含80)以上时,属于醉酒驾车.某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了300辆机动车,查处酒后驾车和醉酒驾车的驾驶员共20人,检测结果如表:
(1)绘制出检测数据的频率分布直方图(在图中用实线画出矩形框即可);
(2)求检测数据中醉酒驾驶的频率,并估计检测数据中酒精含量的众数、平均数.
| 酒精含量(mg/100ml) | [20,30) | [30,40) | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 人数 | 3 | 4 | 1 | 4 | 2 | 3 | 2 | 1 |
(2)求检测数据中醉酒驾驶的频率,并估计检测数据中酒精含量的众数、平均数.
