题目内容
17.平面上一机器人P在行进中始终保持与点F(0,2)的距离比到x轴的距离多2个单位,已知点M(0,-2),当$\frac{|PM|}{|PF|}$的值最大时,$\overrightarrow{PM}$在$\overrightarrow{PF}$上的投影为4.分析 求出P点的轨迹方程,用P的横坐标x表示出$\frac{|PM|}{|PF|}$,求出$\frac{|PM|}{|PF|}$取最大值时P点坐标,得出$\overrightarrow{PM},\overrightarrow{PF}$及其夹角,结合图形计算出投影.
解答  解:设P(x,y),则$\sqrt{{x}^{2}+(y-2)^{2}}=|y|+2$,∴x=0,y≤0或y=$\frac{{x}^{2}}{8}$.
解:设P(x,y),则$\sqrt{{x}^{2}+(y-2)^{2}}=|y|+2$,∴x=0,y≤0或y=$\frac{{x}^{2}}{8}$.
当y≤0时,|PM|≤|PF|,∴$\frac{|PM|}{|PF|}$≤1.
当y>0时,P(x,$\frac{{x}^{2}}{8}$),∴|PM|=$\sqrt{{x}^{2}+(\frac{{x}^{2}}{8}+2)^{2}}$,|PF|=$\sqrt{{x}^{2}+(\frac{{x}^{2}}{8}-2)^{2}}$.
∴($\frac{|PM|}{|PF|}$)2=$\frac{{x}^{2}+({\frac{{x}^{2}}{8}+2)}^{2}}{{x}^{2}+(\frac{{x}^{2}}{8}-2)^{2}}$=1+$\frac{1}{\frac{{x}^{2}}{64}+\frac{4}{{x}^{2}}+\frac{1}{2}}$≤1+$\frac{1}{2\sqrt{\frac{1}{16}}+\frac{1}{2}}$=2.当且仅当$\frac{{x}^{2}}{64}=\frac{4}{{x}^{2}}$即x=±4时取等号.
综上,当P=±4时,$\frac{|PM|}{|PF|}$取得最大值.
不妨x=4,则P(4,2),∴△PFM是等腰直角三角形,∴$\overrightarrow{PM}$在$\overrightarrow{PF}$上的投影为|$\overrightarrow{PF}$|=4.
故答案为:4.
点评 本题考查了平面向量的数量积运算,轨迹方程,两点间的距离公式,基本不等式,属于中档题.

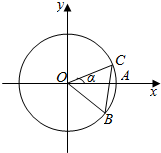 如图,圆O与x轴的正半轴的交点为A,点C、B在圆O上,且点C位于第一象限,点B的坐标为($\frac{12}{13}$,-$\frac{5}{13}$),∠AOC=α,若|BC|=1,则$\sqrt{3}$cos2$\frac{α}{2}$-sin$\frac{α}{2}$cos$\frac{α}{2}$-$\frac{\sqrt{3}}{2}$的值为( )
如图,圆O与x轴的正半轴的交点为A,点C、B在圆O上,且点C位于第一象限,点B的坐标为($\frac{12}{13}$,-$\frac{5}{13}$),∠AOC=α,若|BC|=1,则$\sqrt{3}$cos2$\frac{α}{2}$-sin$\frac{α}{2}$cos$\frac{α}{2}$-$\frac{\sqrt{3}}{2}$的值为( )| A. | $\frac{5}{13}$ | B. | $\frac{12}{13}$ | C. | -$\frac{5}{13}$ | D. | -$\frac{12}{13}$ |
| A. | {1,5} | B. | {1,2,5} | C. | {2,3} | D. | {1,2,3,5} |
| A. | $-\frac{1}{4}$ | B. | $\frac{1}{4}$ | C. | $-\frac{1}{3}$ | D. | $\frac{1}{3}$ |



