题目内容
已知函数f（x）=ax3+bsinx+1（a，b为常熟）且f（5）=7，则f（-5）= ．
考点：函数奇偶性的性质
专题：函数的性质及应用
分析：根据已知条件可以求出a•53+bsin5=6，所以便有f（-5）=-（a•53+bsin5）+1=-5．
解答：
解：f（x）-1=ax3+bsinx；
∴7-1=a•53+bsin5；
∴f（-5）=-（a•53+bsin5）+1=-5．
故答案为：-5．
∴7-1=a•53+bsin5；
∴f（-5）=-（a•53+bsin5）+1=-5．
故答案为：-5．
点评：考查奇函数的定义，并且通过观察f（5）和f（-5）的关系知道求a•53+bsin5即可求出f（-5）．
练习册系列答案
阅读快车系列答案
相关题目
阅读如图所示的算法框图，运行相应的程序，输出的结果是（ ）
| A、-1 | B、2 | C、3 | D、4 |
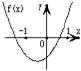函数f（x）=（x-a）（x-b）（其中a＞b）的图象如图所示，则函数g（x）=ax+b的大致图象是（ ）
函数f（x）=
的定义域为（ ）
| ln(4-2x) | ||
|
| A、（-3，2） |
| B、[-3，2） |
| C、[-3，+∞） |
| D、（-∞，2） |