题目内容
【题目】已知![]() 为椭圆
为椭圆![]() 的左右焦点,点
的左右焦点,点![]() 在椭圆上,且
在椭圆上,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过![]() 的直线
的直线![]() 分别交椭圆
分别交椭圆![]() 于
于![]() 和
和![]() ,且
,且![]() ,问是否存在常数
,问是否存在常数![]() ,使得
,使得![]() 等差数列?若存在,求出的值,若不存在,请说明理由.
等差数列?若存在,求出的值,若不存在,请说明理由.
【答案】(1) ![]() ;(2)答案见解析.
;(2)答案见解析.
【解析】试题分析:
(1)由已知可得![]() ,将
,将![]()
![]() 代入
代入![]()
![]() 可得
可得![]() ;
;
(2)①当![]() 的斜率为零或斜率不存在时,
的斜率为零或斜率不存在时, ![]() =
=![]() ;
;
②当![]() 的斜率
的斜率![]() 存在且
存在且![]() 时,
时, ![]() 的方程为
的方程为![]() ,
,
代入椭圆方程![]() ,并化简得
,并化简得![]() .
.
设![]() ,应用韦达定理
,应用韦达定理![]() ,弦长公式
,弦长公式
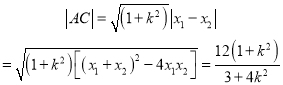
由直线![]() 的斜率为
的斜率为![]() ,得到
,得到 ,计算得到
,计算得到![]() =
= ,求得
,求得![]() .
.
试题解析:
(1)因为![]() ,所以
,所以![]()
所以![]()
![]() ,将P
,将P![]() 代入可得
代入可得![]()
所以椭圆![]() 的方程为
的方程为![]()
(2)①当![]() 的斜率为零或斜率不存在时,
的斜率为零或斜率不存在时, ![]() =
=![]() ;
;
②当![]() 的斜率
的斜率![]() 存在且
存在且![]() 时,
时, ![]() 的方程为
的方程为![]() ,
,
代入椭圆方程![]() ,并化简得
,并化简得![]() .
.
设![]() ,则
,则![]()
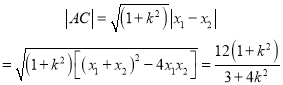
因为直线![]() 的斜率为
的斜率为![]() ,
,
所以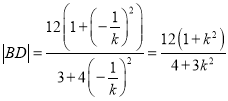
![]() =
=
综上, ![]()
所以,存在常数![]() 使得
使得![]() 成等差数列.
成等差数列.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目


