题目内容
【题目】已知函数
（
）．
（1）若不等式
的解集为
，求
的取值范围；
（2）当
时，解不等式
；
（3）若不等式
的解集为
，若
，求
的取值范围．
【答案】（1）
；（2）
.；（3）
.
【解析】试题分析：（1）对二项式系数进行讨论，可得
求出解集即可；（2）分为
， 
， 
分别解出3种情形对应的不等式即可；（3）将问题转化为对任意的
，不等式
恒成立，利用分离参数的思想得
恒成立，求出其最大值即可.
试题解析：（1）①当
即
时， 
，不合题意；
②当
即
时，
，即
，
∴
，∴
（2）
即
即
①当
即
时，解集为
②当
即
时， 
∵
，∴解集为
③当
即
时， 
∵
，所以
，所以
∴解集为
（3）不等式
的解集为
， 
，
即对任意的
，不等式
恒成立，
即
恒成立，
因为
恒成立，所以
恒成立，
设
则
， 
，
所以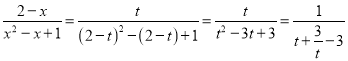
，
因为
，当且仅当
时取等号，
所以
，当且仅当
时取等号，
所以当
时，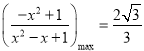 
，
所以
练习册系列答案
相关题目
【题目】为了弘扬民族文化，某校举行了“我爱国学，传诵经典”考试，并从中随机抽取了100名考生的成绩（得分均为整数，满分100分）进行统计制表，其中成绩不低于80分的考生被评为优秀生，请根据频率分布表中所提供的数据，用频率估计概率，回答下列问题．
分组 | 频数 | 频率 |
| 5 |
|
|
|
|
| 35 |
|
| 25 |
|
| 15 |
|
合计 | 100 |
|
（Ⅰ）求
的值及随机抽取一考生恰为优秀生的概率；
（Ⅱ）按成绩采用分层抽样抽取20人参加学校的“我爱国学”宣传活动，求其中优秀生的人数；
（Ⅲ）在第（Ⅱ）问抽取的优秀生中指派2名学生担任负责人，求至少一人的成绩在
的概率．
