题目内容
10.甲、乙两人掷均匀硬币,其中甲掷m次,乙掷n次,掷出的正面次数依次记为x,y.(Ⅰ)若m+n=10,记ξ=x+y,求P(ξ=k)的最大值:
(Ⅱ)若m=3,n=2,求x-y的分布列和数学期望.
分析 (1)利用二项分布即可求出概率,利用二项式系数的性质即得结论;
(2)通过分别求出X的可能取值为-2,-1,0,1,2,3相应的概率,进而可求出X的分布列和数学期望.
解答 解:(Ⅰ)依题意,ξ~B(10,$\frac{1}{2}$),
则P(ξ=k)=${C}_{10}^{k}$$\frac{1}{{2}^{k}}$•$\frac{1}{{2}^{10-k}}$=${C}_{10}^{k}$$\frac{1}{{2}^{10}}$,
由二项式系数的性质可知P(ξ=k)的最大值为${C}_{10}^{5}$$\frac{1}{{2}^{10}}$=$\frac{63}{256}$;
(Ⅱ)由题可知,随机变量X=x-y的可能取值为-2,-1,0,1,2,3,
则P(X=-2)=${C}_{3}^{0}$$\frac{1}{{2}^{3}}$•${C}_{2}^{2}$•$\frac{1}{{2}^{2}}$=$\frac{1}{{2}^{5}}$,
P(X=-1)=${C}_{3}^{0}$$\frac{1}{{2}^{3}}$•${C}_{2}^{1}$•$\frac{1}{{2}^{2}}$+${C}_{3}^{1}$$\frac{1}{{2}^{3}}$•${C}_{2}^{2}$•$\frac{1}{{2}^{2}}$=$\frac{5}{{2}^{5}}$,
P(X=0)=${C}_{3}^{0}$$\frac{1}{{2}^{3}}$•${C}_{2}^{0}$•$\frac{1}{{2}^{2}}$+${C}_{3}^{1}$$\frac{1}{{2}^{3}}$•${C}_{2}^{1}$•$\frac{1}{{2}^{2}}$+${C}_{3}^{2}$$\frac{1}{{2}^{3}}$•${C}_{2}^{2}$•$\frac{1}{{2}^{2}}$=$\frac{10}{{2}^{5}}$,
P(X=1)=${C}_{3}^{1}$$\frac{1}{{2}^{3}}$•${C}_{2}^{0}$•$\frac{1}{{2}^{2}}$+${C}_{3}^{2}$$\frac{1}{{2}^{3}}$•${C}_{2}^{1}$•$\frac{1}{{2}^{2}}$+${C}_{3}^{3}$$\frac{1}{{2}^{3}}$•${C}_{2}^{2}$•$\frac{1}{{2}^{2}}$=$\frac{10}{{2}^{5}}$,
P(X=2)=${C}_{3}^{2}$$\frac{1}{{2}^{3}}$•${C}_{2}^{0}$•$\frac{1}{{2}^{2}}$+${C}_{3}^{3}$$\frac{1}{{2}^{3}}$•${C}_{2}^{1}$•$\frac{1}{{2}^{2}}$=$\frac{5}{{2}^{5}}$,
P(X=3)=${C}_{3}^{3}$$\frac{1}{{2}^{3}}$•${C}_{2}^{0}$•$\frac{1}{{2}^{2}}$=$\frac{1}{{2}^{5}}$,
所以X的分布列为:
| X | -2 | -1 | 0 | 1 | 2 | 3 |
| P | $\frac{1}{{2}^{5}}$ | $\frac{5}{{2}^{5}}$ | $\frac{10}{{2}^{5}}$ | $\frac{10}{{2}^{5}}$ | $\frac{5}{{2}^{5}}$ | $\frac{1}{{2}^{5}}$ |
点评 本题考查概率、随机变量分布列以及数学期望等基础知识,考查运用概率统计知识解决简单实际问题的能力,注意解题方法的积累,属于中档题.


| A. | 3 | B. | 4 | C. | 5 | D. | 6 |

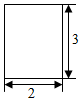
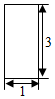
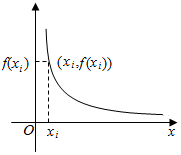 已知函数f(x)=$\frac{1}{x}$(x>0),对于正数x1,x2,…,xn(n∈N+),记Sn=x1+x2+…+xn,如图,由点(0,0),(xi,0),(xi,f(xi)),(0,f(xi))构成的矩形的周长为Ci(i=1,2,…,n),都满足Ci=4Si(i=1,2,…,n).
已知函数f(x)=$\frac{1}{x}$(x>0),对于正数x1,x2,…,xn(n∈N+),记Sn=x1+x2+…+xn,如图,由点(0,0),(xi,0),(xi,f(xi)),(0,f(xi))构成的矩形的周长为Ci(i=1,2,…,n),都满足Ci=4Si(i=1,2,…,n). 为了了解某火车站候车旅客用手机使用火车站WIFI情况,在某日15:00时,把该候车厅10至50岁年龄段的旅客按年龄分区间[10,20),[20,30),[30,40),[40,50]得到如图所示的人数频率分布直方图,现用分层抽样的方法从中得到一样本.若样本在区间[20,30)上有6人,则该样本在区间[40,50]上有4人.
为了了解某火车站候车旅客用手机使用火车站WIFI情况,在某日15:00时,把该候车厅10至50岁年龄段的旅客按年龄分区间[10,20),[20,30),[30,40),[40,50]得到如图所示的人数频率分布直方图,现用分层抽样的方法从中得到一样本.若样本在区间[20,30)上有6人,则该样本在区间[40,50]上有4人.