题目内容
19.已知函数f(x)=ln(x+m)的图象与g(x)的图象关于x+y=0对称,且g(0)+g(-ln2)=1,则m=( )| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
分析 根据函数的对称性求出函数g(x)的解析式,利用方程关系进行求解即可.
解答 解:∵函数y=f(x)=ln(x+m)的图象与g(x)的图象关于x+y=0对称,
∴-x=ln(-y+m),
即-y+m=e-x,
即y=m-e-x,
则g(x)=m-e-x,
∵g(0)+g(-ln2)=1,
∴m-e0+m-e-(-ln2)=1
即m-1+m-2=1,
则2m=4,m=2,
故选:C.
点评 本题主要考查函数对称性的应用,根据函数的对称性求出函数的解析式是解决本题的关键.,(x,y)关于y=x对称的坐标为(y,x),关于y=-x对称的坐标为(-y,-x).

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
14.执行如图所示的程序框图,则下列说法正确的( )
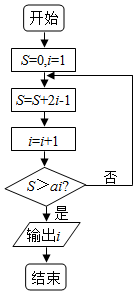

| A. | ?a∈(2,4),输出的i的值为5 | B. | ?a∈(4,5),输出的i的值为5 | ||
| C. | ?a∈(3,4),输出的i的值为5 | D. | ?a∈(2,4),输出的i的值为5 |
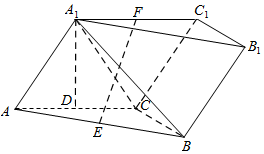 如图,三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,BC=1,且AC⊥BC,点D,E,F分别为AC,AB,A1C1的中点.
如图,三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,BC=1,且AC⊥BC,点D,E,F分别为AC,AB,A1C1的中点. 如图,四边形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1,∠ACB=120°,AB⊥PC,AM=2.
如图,四边形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1,∠ACB=120°,AB⊥PC,AM=2. 如图,已知直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E,F分别是AA1和CC1的中点,且BE⊥B1F.
如图,已知直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E,F分别是AA1和CC1的中点,且BE⊥B1F.
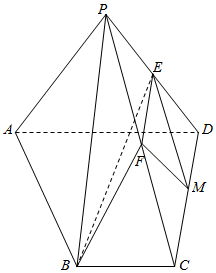 如图所示,已知在四棱锥P-ABCD中,底面四边形ABCD是直角梯形,BC∥AD,BC⊥CD,AD=CD=2BC=4,△PAD是等边三角形,平面PAD⊥平面ABCD,E,F分别是PD,PC的中点,M为CD上一点.
如图所示,已知在四棱锥P-ABCD中,底面四边形ABCD是直角梯形,BC∥AD,BC⊥CD,AD=CD=2BC=4,△PAD是等边三角形,平面PAD⊥平面ABCD,E,F分别是PD,PC的中点,M为CD上一点.