题目内容
 在正方形ABCD中,P是对角线BD上一点,E、F分别在边BC、CD上,且四边形PECF为矩形,用向量方法证明:
在正方形ABCD中,P是对角线BD上一点,E、F分别在边BC、CD上,且四边形PECF为矩形,用向量方法证明:(1)PA=EF;
(2)PA⊥EF.
分析:(1)以B为原点、BC为x轴建立如图直角坐标系,设正方形的边长为1,且BE=x,可得A、B、E、F、P各点的坐标,从而得到
、
的坐标,得到|
|=
且|
|=
,因此得到PA=EF;
(2)根据(1)中的数据,算出
、
的数量积为0,从而得到
⊥
,即AP⊥EF.
| AP |
| EF |
| AP |
| 2x2-2x+1 |
| EF |
| 2x2-2x+1 |
(2)根据(1)中的数据,算出
| AP |
| EF |
| AP |
| EF |
解答:解:以B为原点、BC为x轴,建立直角坐标系,如图所示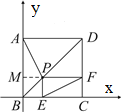
设正方形的边长为1,且BE=x,可得B(0,0),E(x,0),F(1,x),
P(x,x),A(0,1)…2′
可得
=(x,x-1),
=(1-x,x)
(1)根据向量模的公式,得|
|=
=
,|
|=
=
∴|
|=|
|,即AP=EF…6′
(2)∵
=(x,x-1),
=(1-x,x)
∴
•
=x(1-x)+(x-1)x=0
可得
⊥
,即AP⊥EF…10′

设正方形的边长为1,且BE=x,可得B(0,0),E(x,0),F(1,x),
P(x,x),A(0,1)…2′
可得
| AP |
| EF |
(1)根据向量模的公式,得|
| AP |
| x2+(x-1)2 |
| 2x2-2x+1 |
| EF |
| (1-x)2+x2 |
| 2x2-2x+1 |
∴|
| AP |
| EF |
(2)∵
| AP |
| EF |
∴
| AP |
| EF |
可得
| AP |
| EF |
点评:本题在正方形ABCD中,证明线面线段AP与RF垂直且相等,着重考查了正方形的性质和利用向量知识证明平面几何结论的方法,属于中档题.

练习册系列答案
相关题目
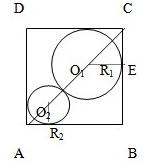 如图,已知正方形的边长为1,在正方形ABCD中有两个相切的内切圆.
如图,已知正方形的边长为1,在正方形ABCD中有两个相切的内切圆. 在正方形ABCD中,E、F分别为AB、BC的中点,用向量求证:AF⊥DE.
在正方形ABCD中,E、F分别为AB、BC的中点,用向量求证:AF⊥DE. 如图,在正方形ABCD中,M是边BC的中点,N是边CD的中点,设∠MAN=α,那么sinα的值等于
如图,在正方形ABCD中,M是边BC的中点,N是边CD的中点,设∠MAN=α,那么sinα的值等于 (2012•武汉模拟)如图,在正方形ABCD中,点E为CD的中点,点F为BC上靠近点B的一个三等分点,则
(2012•武汉模拟)如图,在正方形ABCD中,点E为CD的中点,点F为BC上靠近点B的一个三等分点,则