题目内容
6.在△ABC中,∠BAC=90°,BC=5,D,E为边BC上的两点,且满足:$\overrightarrow{BD}=\frac{1}{3}\overrightarrow{BC},\overrightarrow{CE}=\frac{1}{3}\overrightarrow{CB}$,则$\overrightarrow{AD}•\overrightarrow{AE}$的值为$\frac{50}{9}$.分析 通过建立坐标系,设出B,C坐标,求解D、E坐标,然后向量得到数量积.
解答 解:如图:以A为原点,AB为x轴,AC为:y轴,
设B(3m,0),C(0,3n),9m2+9n2=25,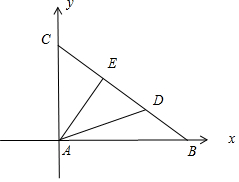
$\overrightarrow{BD}=\frac{1}{3}\overrightarrow{BC},\overrightarrow{CE}=\frac{1}{3}\overrightarrow{CB}$,
则D(2m,n),E(m,2n),
则$\overrightarrow{AD}•\overrightarrow{AE}$=2m2+2n2=2(m2+n2)=2×$\frac{25}{9}$=$\frac{50}{9}$
故答案为:$\frac{50}{9}$
点评 本题考查向量的数量积的应用,向量在几何中的应用,考查计算能力.

练习册系列答案
相关题目
16.完成一项装修工程,请木工共需付工资每人500元,请瓦工共需付工资每人400元,现有工人工资预算20000元,设木工x人,瓦工y人,则工人满足的关系式是( )
| A. | 5x+4y<200 | B. | 5x+4y≥200 | C. | 5x+4y=200 | D. | 5x+4y≤200 |
15.函数f(x)=x2,定义数列{an}如下:an+1=f(an),n∈N*,若给定a1的值,得到无穷数列{an}满足:对任意正整数n,均有an+1>an,则a1的取值范围是( )
| A. | (-∞,-1)∪(1,+∞) | B. | (-∞,0)∪(1,+∞) | C. | (1,+∞) | D. | (-1,0) |
 如图:在一个奥运场馆建设现场,现准备把一个半径为$\sqrt{3}$m的球形工件吊起平放到6m高的平台上,工地上有一个吊臂长DF=12m的吊车,吊车底座FG高1.5m.当物件与吊臂接触后,钢索CD长可通过顶点D处的滑轮自动调节并保持物件始终与吊臂接触.求物件能被吊车吊起的最大高度,并判断能否将该球形工件吊到平台上?
如图:在一个奥运场馆建设现场,现准备把一个半径为$\sqrt{3}$m的球形工件吊起平放到6m高的平台上,工地上有一个吊臂长DF=12m的吊车,吊车底座FG高1.5m.当物件与吊臂接触后,钢索CD长可通过顶点D处的滑轮自动调节并保持物件始终与吊臂接触.求物件能被吊车吊起的最大高度,并判断能否将该球形工件吊到平台上?