题目内容
已知向量
=(cos
x,sin
x),
=(cos
,-sin
),设f(x)=2
•
+m+1(m∈R);
(Ⅰ)求函数f(x)在x∈[0,π]上的单调递减区间;
(Ⅱ)当x∈[0,
]时,-4<f(x-
)<4恒成立,求实数m的取值范围.
| a |
| 3 |
| 2 |
| 3 |
| 2 |
| b |
| x |
| 2 |
| x |
| 2 |
| a |
| b |
(Ⅰ)求函数f(x)在x∈[0,π]上的单调递减区间;
(Ⅱ)当x∈[0,
| π |
| 6 |
| π |
| 6 |
考点:平面向量数量积的运算
专题:导数的综合应用,平面向量及应用
分析:(Ⅰ)先根据条件求出
•
,然后求出f(x),f′(x),根据f′(x)的符号,寻找f(x)在[0,π]上的单调递减区间.
(Ⅱ)根据f(x-
)在[0,
]上导数的符号,从而判断f(x-
)的单调性,从而求出该函数在[0,
]上的取值范围,根据当x∈[0,
]时,-4<f(x-
)<4恒成立,变得出对m限制的式子从而求出m的取值范围.
| a |
| b |
(Ⅱ)根据f(x-
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
解答:
解:(Ⅰ)
•
=cos
x•cos
x-sin
x•sin
=cos(
x+
x)=cos2x;
∴f(x)=2cos2x+m+1,∴f′(x)=-4sin2x;
x∈[0,π],∴2x∈[0,2π];
∴2x∈[0,π],即x∈[0,
]时,f′(x)<0;
∴函数f(x)在x∈[0,π]上的单调递减区间是[0,
].
(Ⅱ)x∈[0,
],∴x-
∈[-
,0],∴2(x-
)∈[-
,0],∴f′(x-
)>0;
∴函数f(x-
)在[0,
]上单调递增,∴f(0-
)≤f(x-
)≤f(
-
);
∴2+m≤f(x-
)≤3+m;
又x∈[0,
]时,-4<f(x-
)<4恒成立;
∴
,解得-6<m<1;
实数m的取值范围是(-6,1).
| a |
| b |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| x |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
∴f(x)=2cos2x+m+1,∴f′(x)=-4sin2x;
x∈[0,π],∴2x∈[0,2π];
∴2x∈[0,π],即x∈[0,
| π |
| 2 |
∴函数f(x)在x∈[0,π]上的单调递减区间是[0,
| π |
| 2 |
(Ⅱ)x∈[0,
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
∴函数f(x-
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
∴2+m≤f(x-
| π |
| 6 |
又x∈[0,
| π |
| 6 |
| π |
| 6 |
∴
|
实数m的取值范围是(-6,1).
点评:熟练掌握两角和的余弦公式,数量积的坐标运算公式,以及求导数判断函数的单调区间的方法.对于第二问的解决思路是判断函数f(x-
)在[0,
]的单调性,根据单调性求f(x-
)的取值范围,再一个需注意的是:在得到f(x-
)的取值范围之后应该如何限制m的取值.
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |

练习册系列答案
相关题目
 如图,三角形ABC中AB=3,AC=6,∠BAC=60°,D为BC中点.
如图,三角形ABC中AB=3,AC=6,∠BAC=60°,D为BC中点. 已知点P是椭圆C上任一点,点P到直线l1:x=-2的距离为d1,到点F(-1,0)的距离为d2,且
已知点P是椭圆C上任一点,点P到直线l1:x=-2的距离为d1,到点F(-1,0)的距离为d2,且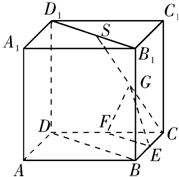 如图所示,在正方体ABCD-A1B1C1D1中,S是B1D1的中点,E、F、G分别是BC、CD和SC的中点.求证:
如图所示,在正方体ABCD-A1B1C1D1中,S是B1D1的中点,E、F、G分别是BC、CD和SC的中点.求证: