题目内容
15.函数y=(x+a)ex在x=0处的切线与直线x+y+1=0垂直,则a的值为0.分析 求函数的导数,根据导数的几何意义结合直线垂直的直线斜率的关系建立方程关系进行求解即可.
解答 解:∵函数y=(x+a)ex在x=0处的切线与直线x+y+1=0垂直,
∴函数y=(x+a)ex在x=0处的切线斜率k=1,
∵f′(x)=(x+a+1)ex,
∴f′(0)=(a+1)e0=a+1=1,
得a=0,
故答案为:0.
点评 本题主要考查直线垂直的应用以及导数的几何意义,根据条件建立方程关系是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.函数f(x)=sinx(sinx+$\sqrt{3}$cosx)的最大值为 ( )
| A. | 2 | B. | 1+$\sqrt{3}$ | C. | $\frac{3}{2}$ | D. | 1 |
10.在年龄互不相同的5名工人中选派工人去看管A、B两个仓库,且两个仓库都至少要有一人看管,若看管仓库A的工人年龄最大的小于看管仓库B的工人年龄最小的,则不同的选派方法有( )
| A. | 45 | B. | 49 | C. | 55 | D. | 59 |
20.直线x-y+4=0被圆(x+2)2+(y-2)2=2截得的弦长等于( )
| A. | $12\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | $3\sqrt{2}$ | D. | $4\sqrt{2}$ |
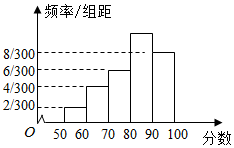 某校为了解一个英语教改实验班的情况,举行了一次测试,将该班30位学生的英语成绩进行统计,得图示频率分布直方图,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
某校为了解一个英语教改实验班的情况,举行了一次测试,将该班30位学生的英语成绩进行统计,得图示频率分布直方图,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].