题目内容

若函数f（x）=
x
(2x+1)(x-a)
为奇函数，则y的值为（　　）
A、
1
2
B、
2
3
C、
3
4
D、1
考点：函数奇偶性的性质
专题：函数的性质及应用
分析：根据函数奇偶性的定义和性质建立方差即可求出a的值．
解答： 解：∵函数f（x）=
x
(2x+1)(x-a)
为奇函数，
∴f（-x）=-f（x），
即f（-x）=
-x
(-2x+1)(-x-a)
=-
x
(2x+1)(x-a)
，
∴（2x-1）（x+a）=（2x+1）（x-a），
即2x2+（2a-1）x-a=2x2-（2a-1）x-a，
∴2a-1=0，解得a=
1
2
．
故选：A．
点评：本题主要考查函数奇偶性的定义和性质的应用，利用函数奇偶性的定义建立方程是解决本题的关键．
练习册系列答案
相关题目
下列命题：
①已知数列{an}，an=
1
n(n+2)
（n∈N*），那么
1
120
是这个数列的第10项，且最大项为第1项；
②数列
2
，
5
，2
2
，
11
，…的一个通项公式是an=
3n-1
；
③已知数列{an}，an=kn-5，且a8=11，则a17=29；
④已知an=an+1+5，则数列{an}是递减数列．
其中真命题的个数为（　　）
A、4B、3C、2D、1
若△ABC的两个顶点坐标A（-4，0）、B（4，0），△ABC的周长为18，则顶点C的轨迹方程为
 
．
圆心在直线2x+y=0上，且与直线y=1-x相切于点（2，-1）的圆的标准方程为
 
．
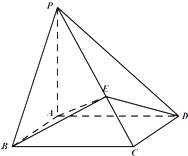在四棱锥P-ABCD中，PA⊥平面ABCD，四边形ABCD为平行四边形，AB=1，BC=
2
，∠ABC=45°，点E在PC上，AE⊥PC．
（1）证明：AE⊥平面PCD；
（2）当PA=2时，求直线AD与平面ABE所成角的正弦值．（请用向量的运算解决此问题）
集合M={x|x2＜3x}，N={x|x3≤8}，则M∩N=
 
．
如果θ∈（
π
4
，
π
2
），且sinθ+cosθ=
7
5
，那么tanθ=
 
．
已知α满足f（α）=
sin(α-
3π
2
)cos(
π
2
+α)tan(π-α)
tan(α-π)sin(π-α)

（1）化简f（α）；
（2）若cos（α-
3π
2
）=
1
3
，α∈（π，
3π
2
），求f（α+
π
4
）的值；
（3）若f（α）=2f（α+
π
2
），求sin2α+2sinα•cosα的值．
某班60名同学参加高中数学毕业会考所得成绩（成绩均为整数）整理后画出的频率分布直方图，求该班及格（60分以上）的同学的人数？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网