题目内容
若关于x的不等式x2+|x+3a|<2至少有一个正数解,则实数a的取值范围是( )
A、(-
| ||||
B、(-
| ||||
C、(-
| ||||
D、(-
|
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:将原不等式变形为:|x+3a|<2-x2,我们在同一坐标系画出y=2-x2(y>0,x>0)和 y=|x|两个图象,利用数形结合思想,易得实数a的取值范围.
解答:
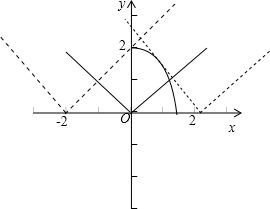 解:原不等式变形为:|x+3a|<2-x2,且 0<2-x2.
解:原不等式变形为:|x+3a|<2-x2,且 0<2-x2.
在同一坐标系画出y=2-x2(y>0,x>0)
和 y=|x|两个函数图象,
将绝对值函数 y=|x|向左移动当右支经过 (0,2)点,
可得-3a=-2,求得a=
.
将绝对值函数 y=|x|向右移动让左支与抛物线y=2-x2
(y>0,x>0)相切时,
由
可得x2-x-3a-2=0,由判别式△=0,
求得a=-
.
数形结合可得,实数a的取值范围是(-
,
),
故选:D.
 解:原不等式变形为:|x+3a|<2-x2,且 0<2-x2.
解:原不等式变形为:|x+3a|<2-x2,且 0<2-x2.在同一坐标系画出y=2-x2(y>0,x>0)
和 y=|x|两个函数图象,
将绝对值函数 y=|x|向左移动当右支经过 (0,2)点,
可得-3a=-2,求得a=
| 2 |
| 3 |
将绝对值函数 y=|x|向右移动让左支与抛物线y=2-x2
(y>0,x>0)相切时,
由
|
求得a=-
| 3 |
| 4 |
数形结合可得,实数a的取值范围是(-
| 3 |
| 4 |
| 2 |
| 3 |
故选:D.
点评:本题主要考查二次函数的图象,及绝对值函数图象,其中在同一坐标中,画出y=2-x2(y>0,x>0)和 y=|x|两个图象,体现了数形结合的思想,属于中档题.

练习册系列答案
相关题目
设F1,F2分别是双曲线
-
=1(a>0,b>0)的左、右焦点,若双曲线左支上存在一点M使
•(
+
)=0,O坐标原点,且|
|=
|
|,则该双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| F1M |
| OM |
| OF1 |
| MF1 |
| ||
| 3 |
| MF2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知{an}是等比数列,a1=2,a4=16,则公比q等于( )
A、
| ||
B、
| ||
| C、2 | ||
| D、4 |
已知F1(-3,0),F2(3,0),是椭圆
+
=1(a>b>0)两个焦点,P在椭圆上,∠F1PF2=α,且当α=
时,△F1PF2的面积最大,则椭圆的标准方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 2π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
直线
(t为参数)的倾斜角为( )
|
| A、30° | B、60° |
| C、90° | D、135° |
已知i是虚数单位,则
=( )
| 2+i |
| 1+i |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|