题目内容

精英家教网函数y=tan(
πx
4
-
π
2
)（1＜x＜4）的图象如图所示，A为图象与x轴的交点，过点A的直线l与函数的图象交于B，C两点，则（
OB
+
OC
）•
OA
=（　　）
A、-8B、-4C、4D、8
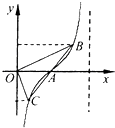
分析：先确定点A（2，0）再射出点B（x1，y1），C（x2，y2），由题意可知点A为B、C两点的中点，故x1+x2=4，y1+y2=0．将点B、C代入即可得到答案．
解答：解：由题意可知 B、C两点的中点为点A（2，0），设B（x1，y1），C（x2，y2），则x1+x2=4，y1+y2=0
∴（
OB
+
OC
）•
OA
=（（x1，y1）+（x2，y2））•（2，0）=（x1+x2，y1+y2）•（2，0）=（4，0）•（2，0）=8
故选D．
点评：本题主要考查平面向量的数量积运算．属基础题．
练习册系列答案
相关题目
函数y=tan(x+
π4
)的定义域为
 
．
给出下列命题：
①若
a
≠
0
，则“
a
•
b
=
a
•
c
”是“
b
=
c
”成立的必要不充分条件
②若
a
=(3，4)，
b
=(0，-1)，则
a
在
b
方向上的投影是-4
③函数y=tan(x+
π
3
)的图象关于点(
π
6
，0)成中心对称
④“一个棱柱的各侧面是全等的矩形”是“这个棱柱是正棱柱”的充要条件
其中真命题是
 
．
下列命题为真命题的是（　　）
函数y=tan(x+
π
3
)的图象的对称中心的坐标是（　　）
A、(kπ-
π
3
，0)，k∈Z
B、(
kπ
2
-
π
3
，0)，k∈Z
C、(
kπ
2
，0)，k∈Z
D、（kπ，0），k∈Z
（2012•株洲模拟）已知函数y=tanωx（ω＞0）的图象与直线y=a相交于A，B两点，若AB长度的最小值为π，则ω的值为（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网